Aggregation and Composition

Contents

0. Introduction
1. A first example showing both aggregation and composition
2. A second example showing both aggregation and composition

0. Introduction

Aggregation and composition are specialised forms of association, both used when we can consider objects of one class to be a part of another.  Composition is stronger than association in that when the owning object dies, the parts must die too.

Aggregation is represented by a open diamond and composition by a black diamond. 

A developer can arguably ignore the notion of aggregation if he/she doesn't think it amounts to much. It's just a nice thing to have if people drawing diagrams think that it lends more meaning to what they're drawing.  Composition, however, is much more significant, due to the coincident lifetimes of both the whole and the parts.  

1. A first example showing both aggregation and composition:

Question:  Explain all the syntax on the diagram below (Figure 1) and its semantics.

Answer: The diagram below shows an example of both aggregation (unfilled-in diamond) and composition (filled-in diamond).  Note, incidentally, that we've an opportunity to revise other elements of UML syntax here. 

We'll describe all aspects of the diagram, including as we do so the ideas of aggregation and composition.

1. From the arrow on the association between Polygon and Point, we realise that a polygon knows of its Points but each Point doesn't know to which Polygon, if any, it belongs. 

This means that we can send a message to a polygon of the sort:

List polyVertices = largePolygon.whatAreYourVertices( );

but that you can't send a message like this to a Point object, p1:

Polygon poly = p1.whatPolygonIfAnyDoYouBlongTo( );

2. Note the constraint {ordered}.  As you already know, a constraint is always placed between curly brackets.  In forming a polygon the order of the Points is critical, since more than one polygon could have exactly the same set of vertices (i.e. corners).  A Polygon is composed of three or more Points, whereas a Circle is composed of only one, representing its centre.  When a Polygon or a circle dies its Point objects die too.  A style is also part of a Circle or a Polygon but a style definition can live on even if the Polygon or the Circle dies.  It's certainly valid to use composition for the Point objects.  It's generally debatable whether aggregation is worth distinguishing from ordinary association.  We might argue that it's worthwhile here if only to indicate that a Style is part of a Circle or a Polygon.  Remember that the words is part of forms the essence of what aggregation and composition are all about. 

Figure 1

An alternative way of representing the above information is shown below. 

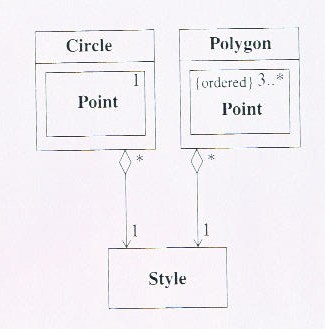
Figure 2

or we could modify Figure 2 to show the contained Point parts, using conventional attribute notation, such as, in the case of Circle

centre : Point [1]

2. A second example showing both aggregation and composition:

Question: Explain all the syntax on this diagram (Figure 3) and its semantics.

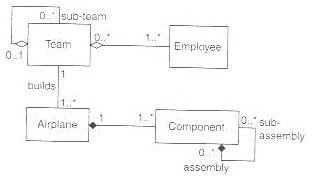
Figure 3

Answer: The diagram above shows (a) ordinary association, (b) aggregation and (c) composition.  As you know already, both aggregation and composition are used when the vocabulary “is a part of” can be used.  We can say that Employees are part of a team but not that Airplanes are part of a team nor that a Team is part of an Airplane.  Composition (solid black diamond) is a stronger form of “is part of” than aggregation.  With composition, the two ends of the association have coincident life times.  When an airplane is disposed of, so are its components.  Of course some of the components may be reused and put into the spare parts store, but they cease to be of any interest to us and our own chunk of software being modelled here. 

Components may consist of components and those in turn may consist of components until they bottom out into irreducible components.  Thus a component can play the role of “assembly” or of “sub-assembly”.  Hence the role names at each end of the association between the component class and itself.  Note also that a team may play the role of sub-team. 

Note that we can infer things about the domain from this diagram.  For example, a team continues to exist even when the superteam of which it may be a part is dissolved.  This is implied by the use of aggregation, in the top left corner, rather than composition.  The reasons for this could be that a team may be part of more than one superteam, or may continue to exist simply because its team members have worked together for years and may be given other projects on which to work together. 

In short: 

When a superteam dies, the subteam doesn’t generally die (aggregation).

When a airplane dies, its components die too (composition).

When a component dies, its own components die too (composition).  This cascades all the way down the component/subcomponent chain.