PROLOG Summary Volume 1

These notes are based on ones originally written by Mairead Meagher, to whom thanks are due. I've modified them to suit this web site. Please attribute any deficiencies or errors to me, not to Mairead!

(Volume two obtainable by clicking at the link at the end)
 
 

Prolog Part 1

Introduction

The idea of Prolog is to use logic as a programming language. Prolog is suited to problems

• that involve objects and the relationships between them
• non-numerical computations

Traditional programming involves writing a procedure with an explicit sequence of steps.

Prolog programming involves

1. declaring a set of facts and
2. writing rules that define relationships

So, writing a program in Prolog consists of

1. Declaring facts about entities and their relationships e.g. John is a brother of Mary, Blackie is a white cat, etc.
2. Declaring rules about entities and their relationships, e.g. (i) two people are brothers if ... (ii) a cat is lucky if ...

Using a Prolog program consists of

Asking questions about the entities and relationships e.g. who is John’s brother?, who is a lucky cat?
 

Example

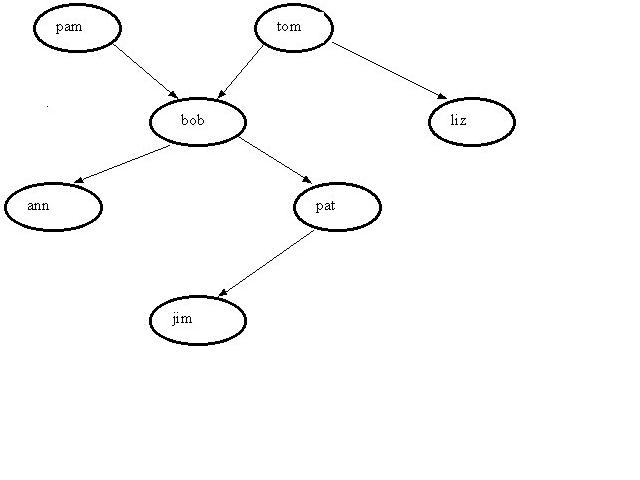
To find out who are whose grandchildren given a set of facts and rules..

We have the following facts:

Pam is the parent of Bob.
Tom is the parent of Bob.
Tom is the parent of Liz.
Bob is the parent of Ann.
Bob is the parent of Pat.
Pat is the parent of Jim.

We have the following rule:

X is a grandparent of Z if X is a parent of Y and Y is a parent of Z.

We then have a question : List out Tom’s grandchildren given the above information.

We have a family tree that looks like:

The Prolog program would look like:

parent(pam, bob).
parent(tom, bob).
parent(tom, liz).
parent(bob, ann).
parent(bob, pat).
parent(pat, jim).
grandparent(X, Z) :- parent(X, Y) , parent(Y, Z).

This program will be contained in an ordinary text file, edited, on the VAX, using one of the standard editors.. To see the program in use, on the VAX, the user types setup pop, after the $ prompt followed by prolog

i.e.

$setup pop(return key pressed)
$prolog (return key pressed again)

The prompt changes from $ to ?-, which is the Prolog system's way of saying "Ask me a question." The first question we ask is

consult('family.pr'). if, say, the program above, in brown, were in the file family.pr. This is typed after the ?- prompt, i.e.

?-consult('family.pr').

The user now interacts with the program. Computer's text is in red; the user's in blue.

?- grandparent(tom, Z).

This will give you the following answer:

Z = ann ? y (Go again prompt)
Z = pat ? y(Go again prompt)
no
?-

?-grandparent(tom,ann).

This will give you the following answer:

yes ? y
no

?-grandparent(tom,bob).

This will give you the following answer:

no ? y
no

Important Point: From the three questions above, it can be seem that if a question is asked with a variable in it, then the computer will try to provide values that satisfy the variable in such as way as to make the question true. If however, there are no variables in the question, the user is asking something that has a yes/no answer.

When the user is finished asking questions, he/she types halt. and the computer reverts to $

i.e.

?-halt.
$

(Other computers have slightly different ways of providing a Prolog system. For example, you wouldn't use the setup pop command on a PC.)

What is a fact in Prolog?

Anwer: a statement that some thing (or entity) has a particular property or that some relationship holds between two things. Facts are expressed by applying a predicate to a list of arguments (arguments are what's in the brackets, so to speak).

property(entity name). e.g. cow(daisy). meaning Daisy is a cow.
relationship(entity names separated by two commas). eat(cows, grass). meaning Cows eat grass.

Conventions:

• A predicate with one argument, p(e) usually means that the entity e has a property/attribute p ( e.g. woman(pam) means pam is a woman)
• A predicate with two arguments in the form r(a,b) means that a stands in relation r to b (e.g. parent(pam, bob) means pam is bob’s parent).

parent(pam, bob).
parent(tom, bob).
parent(tom, liz).
parent(bob, ann).
parent(bob, pat).
parent(pat, jim).

To ask a question ‘Is pam bob’s mother ? ‘, we type the following:

?- parent(pam, bob).Note the full stop.
yes
?-

(you must know the structure of the facts to get the right answer)

To check is pam a mother, type

?- mother(pam).
no
?-

(The fact does not exist in the database as given so no is returned)

Question :

To whom is Tom a grandparent? Here we must use a variable in the question.

Prolog variables MUST begin with a capital letter. Constants, on the other, hand MUST NOT.

?- grandparent(tom, Z). Don't forget that what the computer says in is red and what the user says is in blue.
Z = ann ? y (Go again prompt)
Z = pat ? y (Go again prompt)
no
?-

Question :

Who are pat’s grandparents?

?- grandparent(X, pat).
X = pam ? y (Go again prompt)
X = tom ? y (Go again prompt)
no
?-

Exercises:

1. Write down a rule for two people being siblings.
2. Write down a rule for two people being sisters (you will need to create a new predicate).
3. Write down a rule for people being either siblings or first cousins.
4. Write the following assertions as Prolog statements:

• betty is a dog
• Mary's father is Paul

Some of the answers are at bottom of page. Click here!

Using the Prolog program as before:

parent(pam, bob).
parent(tom, bob).
parent(tom, liz).
parent(bob, ann).
parent(bob, pat).
parent(pat, jim).

we discuss the following:

A conjunction of goals is represented by placing a comma between the goals and is read as and.

It may be used interactively, e.g.

Is tom liz’s parent and is bob ann’s parent?

?- parent(tom, liz), parent(bob, ann).
yes

If I wish to ask "What child do both tom and pam have?"

?- parent(tom, X), parent(pam, X).
X = bob ? y
no

Her is another example:

plays(john, basketball).
plays(mary, tennis).
plays(john, soccer).
plays(mary, soccer).

A disjunction of goals is indicated by a semicolon and read as or.

"Does john play rugby OR does mary play soccer?"

?- plays(john, rugby);plays(mary, soccer).
yes

Remember that what you've just read in red and blue is not a program but rather a use, by the user of the Prolog Program in brown.

Note that the comma (standing for AND) has (just as in C++, and most, if not all, other computer languages) a higher precedence than the semicolon (OR).

"Does john play soccer and rugby OR does mary play basketball?"

?-plays(john, soccer), plays(john, rugby); plays(mary, basketball).
no
?- plays(john, soccer); plays(john, rugby), plays(mary, basketball).
yes

Predicates may be defined in the following ways:

• by a complete list of all the facts in which they occur;
• by general rules;
• by a combination of facts and rules.

The syntax for a Prolog rule is as follows:

head of rule :- body of rule.

where ‘:-’ is read as if, i.e. the head of the rule is true if the body is true.

Example Program

likes(tom, wine).
likes(tom, food).
likes(john, food).
likes(john, wine).
likes(john, mary).
likes(john, Y) :- likes(Y, wine), likes(Y, food). /*john likes anyone(X) who likes food and wine. */

User Interaction with the Example Program

?-likes(john, What).
What = food ? y
What = wine ? y
What = mary ? y
What = tom ? y
What = john ? y
no

Summary of syntax rules:

At the beginning of your use of Prolog, many of your problems may be simple syntax errors. A few main points to look out for:

1. Incorrect use of capital letters. Remember that capitals are reserved for use as the initial characters in variables and that anything starting with a capital is taken to be a variable. For example, X, Y, What, Who Something are all taken to be variables. A variable can also begin with an underscore, e.g. _x , _something.

2. Assertions and rules MUST terminate with a full stop. Failure to add one accounts for a high percentage of errors when the language is first being used.

3. Mistaken Inversion of logical meaning. Remember Prolog believes exactly what you say. It doesn't have the intelligence to figure out what you wanted to say. The only facts it knows are supplied by you, so be careful! e.g. person(mary) can be interpreted as ‘mary is a person’ . However, if you choose to write mary(person), this is syntactically correct. It means something strange (‘person is a mary’?) and something you probably don’t mean to say, so be careful!

Much the same applies to formulating rules i.e. the dominant part of the rule is to the left e.g.

dog(X) :- carnivore(X).

states that X is a dog if X is a carnivore. This implies that all carnivores are dogs. This is not the case, since, for example, people, though they're not dogs, are often carnivores.

carnivore(X) :- dog(X).

however, states that X is a carnivore if X is a dog. This is the case.

4. The comma is an important part of the language used in two ways:-

(i) inside a bracket, it separates two or more subjects or variables, e.g. parent(tom,bob).
(ii) Used outside a set of brackets, it means and e.g.

lucky(X) :- black(X), cat(X).

i.e. X is lucky if X is black and X is a cat.

5. The use of or in rules.

If we wish to give a rule for any X being lucky in one of two cases, we can do this in two ways:

(a)

lucky(X) :- cat(X), black(X).
lucky(X) :- sheep(X), black (X).

There are two rules. If the first one (black cat) does not prove true, Prolog will go onto the next rule (black sheep). This simulates an or.

(b)

We can use the or ‘;’ character to collapse the two rules into one as in:

lucky(X) :- (cat(X) ; sheep(X) ), black(X).

i.e. X is lucky if (either X is a cat or X is a sheep) and X is black.

Severe Warning:

On the basis of the Summer Examination performance in 2001, it is clear that there is confusion about the blank variable, about which a discussion follows. Those resitting in September should be VERY careful to study the following material:

The use of the blank variable:

We have already seen that a variable can begin with an underscore. The underscore can also be used to represent a blank variable. The blank variable is used when we need to recognise the existence of an argument, but we do not need to instantiate it to a constant value. For example:

husband(X) :- married(X, _).

We are saying here that X is a husband if X is married to anyone, whose identity we do not need to know. All we need to know is that that person exists.

Let use place this in context:

married(brendan, anne). /*Assertions in the form married(man, woman) */
married(pat, mary).
married(gerard, catherine).
child(brendan, anne, john).
child(mary, pat, james).
male(john).
male(james).
son(X) :- child(_, _, X), male(X).
husband(X) :- married(X, _).
wife((X) :- married(_,X).

Let us simulate a question and answer session using the example program above.

The setup pop and so on (or whatever is appropriate to your own brand of computer) is done and then the following discussion takes place between user and computer where the computer's getting its knowledge from the file with the brown text in it.

?- husband(X). /* Who is a husband? */
X = brendan ? y
X = pat ? y
X = gerard ? y
no
?- son(john). /* Is john a son ?*/
yes
?- child(_, _, X). /* List all children */
X = john ? y
X = james ? y
no
?- married(_, catherine). /* Is catherine married? */
yes
?- married(_, X). /* Who is married? */
X = anne ? y
X = mary ? y
X = catherine ? y
no
?- married(_, _, _). /* Is anyone married? */
yes
?- /*end of session*/

Arithmetic

The is Operator (This is Prolog's equivalent of C++'s assignment operator =)

The expression A is B-1 has the effect of assigning to variable A one less than the contents of B.

The operators used are

+ addition
- subtraction
* multiplication

If we use more than one operator, the usual precedence rules apply. For example multiplication is done before addition and so on.

Recursion in Prolog

If we revisit the parent/grandparent example that we have already seen, remembering that given the parent facts, the rule for grandparent is:

grandparent(X, Y) :- parent(X, Z), parent(Z, Y).

and if we extend this to the definition of great grandparent, it becomes:

greatgrandparent(X, Y) :- parent(X, M), parent(M, Z), parent(Z, Y).

and so on

Each of these people could be generically described as predecessors, so

predecessor(X, Y):- parent(X, Y).
predecessor(X, Y):- parent(X, Z), parent(Z, Y).
predecessor(X, Y):- parent(X, M), parent(M, Z), parent(Z, Y).

and so on -

We could more succinctly describe the predecessor as follows:

for all X and Y, X is a predecessor of Y if there is a Z such that:

(1) X is a parent of Z and
(2) Z is a predecessor of Y.

A Prolog rule in this form would look like:

predecessor(X, Y) :-parent(X, Z), predecessor(Z, Y).

We need the direct predecessor rule also:

predecessor(X, Y) :-parent(X, Y).

The full rule is as follows:

predecessor(X, Y) :-parent(X, Y).
predecessor(X, Y) :-parent(X, Z), predecessor(Z, Y).

Note that the order is very important, i.e. the 'exit' clause must be first. This definition is called recursive because, in defining a predecessor, we use predecessor.

Recursion in arithmetic:

if we examine the factorial problem, N! (read N factorial) is:

N! = N * (N-l) *(N-2) * (N-3) * (N- 4) ...... * 2 * 1

This can also be written recursively as N! =N*(N-1)! with the exit clause: 1! =1 To write this in Prolog, firstly use the exit clause:

factorial(1, 1):- !.1*1!is one. Once we've got here, stop, i.e. N! has one answer*/
factorial (N, A):- M is N-1, factorial (M, B), A is B * N. /*You can easily see that this really is just another way of saying N! =N*(N-1)!

Note that the ! sign in the above predicate has nothing remotely to do with the ! sign in ordinary mathematics. It's just a coincidence that in writing the predicates for factorial, we end up using the ! sign in Prolog. In the program above it (i.e. !) prevents the computer from running down into the negative numbers and going on forever.

Answers to the following exercises:

1. Write down a rule for two people being siblings.
2. Write down a rule for two people being sisters (you will need to create a new predicate).
3. Write down a rule for people being either siblings or first cousins.
4. Write the following assertions as Prolog statements:

• betty is a dog
• Mary's father is Paul

brother(X,Y):-parent(Z,X),parent(Z,Y),male(X). X is Y's brother if they have at least one parent in common, i.e. half or full brother. You'd have to write the predicate differently if only full brothers could be regarded as brothers. As always it depends on what the customer wants.
sister(X,Y):-parent(Z,X),parent(Z,Y),female(X). // note that Y can be male or female; it's X who's the sister of Y.
sibling(X,Y) :- brother(X,Y);sister(X,Y). note that this rule only works if the previous two rules have been written.
*note the ; operator meaning or.* sibling if brother or sister.

dog(betty). betty is a dog. Note that we must write betty, not Betty, since only variables begin with an upper case letter.
father(paul,mary). paul is the father of mary. Again lower case rather than upper since only variables begin with upper case letters.

Try first cousins, now; that will depend on having at least one grandparent in common, or even both, depending on what exactly first-cousin means.

Go back to the exercises.

On to the next part of these notes
Back to Ian Downey's courses home page