Circles For Leaving Certificate Honours Mathematics
(Thomas O’Sullivan 1997)

 

A circle is a set of points each of which is equidistanced (the radius) from a fixed point (the centre).

 

1. Equation of a circle centre (0,0) and radius R. (fig. 1)

We use pythagorus theorem on the triangle defined by the point (x,y) and the two axes

x2 + y2 = R2

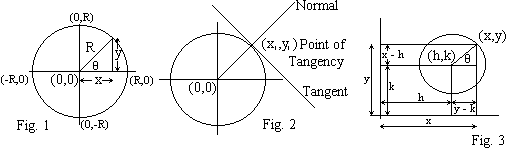
2. To find the equation of a tangent to a circle centre (0,0) and radius R at the point (x1,y1).

A tangent is a line which touches a circle at one point (called the point of tangency) only.

A normal is a line which goes through the centre of a circle and through the point of tangency.

(N.B. The normal is always perpendicular to the tangent).

a). Find the slope of the normal. (Slope formula). Here mn = .

b). Find the slope of the tangent. (Perpendicular to the tangent). Here mt = -.

c). Find the equation of the tangent. (y - y1 = m(x - x1)). Here

y - y1 = -(x - x1)

yy1 - y1y1 = -xx1 + x1x1

xx1 + yy1 = But as (x1, y1) is on the circle = R2

xx1 + yy1 = R2

 

3. The equation of a circle centre (h,k) and radius R. From fig. 3 we see that pythagorus’

theorem applied to the right angled triangle gives

(x - h)2 + (y - k)2 = R2

4. To find the equation of a tangent to a circle centre (h,k) and radius R at the point (x1,y1).

a). Find the slope of the normal. (Slope formula).

b). Find the slope of the tangent. (Perpendicular to the tangent).

c). Find the equation of the tangent. (y - y1 = m(x - x1)). Here

 

5. To find the point of intersection of a circle and a line.

(i) From the line get a value of y (or x) in terms of x (or y).

    1. Put this value of y (or x) into the circle. This gives a quadratic equation. Solve and put the value(s) back into the equation of the line to give the point(s).
    2. If there is only one answer then the line is a tangent. Two answers and the line is a chord. A complex number answer means the line and the circle did not intersect.

 

6. Circles in the form x2 + y2 + 2gx + 2fy + c = 0

If we square out (x - h)2 + (y - k)2 = R2 we get

x2 - 2hx + h2 + y2 - 2ky + k2 = R2

Rearranging x2 + y2 - 2hx - 2ky + h2 + k2 - R2 = 0

Comparing this with x2 + y2 + 2gx + 2fy + c = 0 we see that

h = -g and k = -f also h2 + k2 - R2 = c

therefore R2 = h2 + k2 - c

but a h = -g and k = - f we get

R =

7. To show the position of a point relative to a circle.

(i). A point is inside a circle if the distance from the centre to the point is less than R.

(ii).A point is on a circle if the distance from the point to the centre is equal to the radius.

(iii). A point is outside a circle if the distance from the point to the centre is greater than R.

 

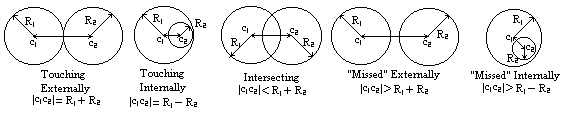
8. Touching circles

    1. Two circles touch externally if the distance between their centres is equal to the sum of their radii.
    2. Two circles touch internally if the distance between their centres is equal to the difference between their radii.
    3. Two circles intersect if the distance between their centres is less than the sum of their radii.
    4. Two circles do not touch and are external to each other if the distance between their centres is greater than the sum of their radii.
    5. Two circles do not touch and one is contained in the other if the distance between their centres is less than the difference between their radii.

9. If the equation of two circles are treated as two simultaneous equations and the squares cancelled out, the remaining equation is the equation of either the common chord, common tangent or another line, depending on the nature of the two circles (i.e. point 6 above.)

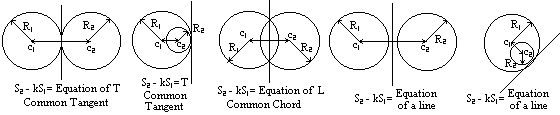
10. Given three points on a circle, to find the equation of the circle:

(i). Let x2 + y2 + 2gx + 2fy + c = 0 be the equation of the circle.

(ii). Put each of the given points into this equation to give 3 simultaneous equations.

(iii). Solve the three equations to give values for g, f and c.

    1. put these values back into x2 + y2 + 2gx + 2fy + c = 0 to give the required equation.

11. Given two points on a circle and a line through the centre, to find the equation of the circle.

(i). Let x2 + y2 + 2gx + 2fy + c = 0 be the equation of the circle.

(ii). Put each of the given points into this equation to give 2 simultaneous equations.

(iii). Put (-g, -f) into the given line to give a third equation.

(iii). Solve the three equations to give values for g, f and c.

    1. put these values back into x2 + y2 + 2gx + 2fy + c = 0 to give the required equation.

12. To find the length of a tangent from a given point to a circle.

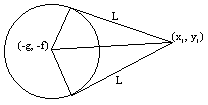
    1. Find the distance from the point (x1,y1) to (-g,-f) using

(ii)This distance is the hypotenuse of a right angled triangle.
    1. Using pytahgorus’ theorem we get

L2 + R2 =

    1. but as R =
we get

L2 =

L =

13. To prove a given line is a tangent to a circle:

    1. Find the perpendicular distance from the line to the centre of the circle.
    2. Find the radius of the circle
    3. If (i) = (ii), then the line is a tangent.

 

14. To find the equations of the tangents to a circle from a given point.

(i). The equation of any line through the point (x1,y1) can be written

y - y1 = m(x - x1) where m, the slope, is unknown.

We will write this line as mx - y + k = 0. (Note, in practice k would be known).

(ii). The perpendicular distance from this line to the centre of the circle is equal to the radius.

i.e. 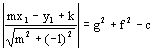(the perpendicular distance formula )

(iii). Solving this gives two values of m which can be used to find the two tangents. (The diagram in 10 above, shows the position of the two tangents.)

15. Orthoganol circles: Two circles are orthagonal if the the tangents to each circles at the points of intersection go through the centres of the other circle.

OR

Two circles are orthagonal if the tangent to one circle is a normal to the other.

From the diagram, (distance between the centres)2.

Which gives the condition for orthagonality

2g1g2 +2f1f2 = c1 + c2

 

16. Parametric equation of circles

In fig. 3 above we see that cosq = and sinq =

This gives x = Rcosq + h and y = Rsinq + k.

As these are equations expressed in terms of a third variable, q , this is the parametric equation of a circle, centre (h,k) and radius R.

To convert a circle given in parametric form to a circle in cartesian form:

  1. Find values for sinq and cosq .
  2. Using the fact that sin2q + cos2q = 1, put in the values for sinq and cosq obtained in 1.
  3. Manipulate formula to write the circle in the form x2 + y2 + 2gx + 2fy + c = 0.

Return to Thomas O'Sullivan's Homepage