Integration types for Leaving Certificate Maths

Integration Types for Leaving cert. Honours Mathematics

Thomas O'sullivan 1997
Integration Types

The following are 20 integration types essential for question 8 on both papers I and II of the Leaving Certificate Honours Mathematics Examination.

1. y =ò(axⁿ + bx^n-1 + cx^n-2 +....)dx y = ò(2x³ + 4x² + 6x)dx

2. y = ò(2x + 3)⁴dx (Let u = 2x + 3)

3. (Let u = x²+ 1)

4. y = ò(2x + 1)(2x - 4)³dx (Let u = 2x – 4 and find a value for 2x +1 in terms of u)

5. y = òsin mx dx or òcos mx dx or .... (let u = mx)

6. y = òsin 3x cos x dx .....(change to sum) note also òsin²xcos²x dx

7. y = òsin²x dx = ò½ ( 1- cos 2x)dx or y = òcos²x dx

8. y = òsin²xcos³x dx... (Cos³x = cos x (1 - sin2x))

9. y = òe^nxdx (Let u = nx)

10. e.g. or y = ò tan x dx …….solution in the form log_e f(x) + c

(let u = denominator)

11. Divide numerator by denominator

12. (Let u = logex )

also (Let )

13. 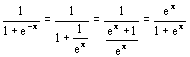() (Let u = 1+e^x)

14. y = ò 2^x dx let u = 2^x then log_eu = x log_e2 differentiating gives

which implies that dx substitute ....

15. is a sin^-1x problem

16. becomes (tan^-1 function) (Let u = x –1)

17.

(Let u = x + 1) (sin^-1 function)

18. (Let )

19. and (Let u = sin x) (tan^-1 function)

Integration by parts is examinable on paper II in the option section:

20. y = òx² log_ex dx; y =òxcos2x dx; y = òx²e^4xdx; y = òx²sinx dx; y = òe^2xsinx dx By parts.

Remember, the order of substitution is given by: L I A T E; Logs, indices, algebra, trigonometry and exponentials

^{© T O’Sullivan A Phabolous FIsics Production™ January 1994

Return to Thomas O'Sullivan's Homepage}