To find the length of a line with the points a(x1,y1) and b(x2,y2) we use the following formula:
Example:
Find the distance from a(-1,6) and b(-3,2)
| a(-1,6) b(-3,2) | » write down values |
| (x1,y1) (x2,y2) | of (x1,y1) & (x2,y2) |
| » write out the formula | |
| » sub in the values | |
| » work it out | |
|
|
» work it out |
|
|
» Distance |
![]()
The midpoint gives the exact point between a(x1,y1) and b(x2,y2). The formula is fairly straightforward and is easy to use:
Example:
Find the midpoint between a(-1,2) and b(3,-6)
| a(-1,2) b(3,-6) | » write down values |
| (x1,y1) (x2,y2) | of (x1,y1) & (x2,y2) |
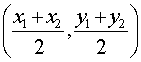 |
» write out the formula |
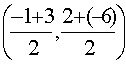
|
» sub in the values |
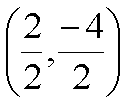 |
» work it out |
|
|
» Midpoint |
Midpoint = (1,-2)
![]()
Show that a point is on a line
To show that a point is on a line all you have to do is:
Sub the point you are given into the line.
Example:
Show that the point a(-3,4) is on the line L:2x+5y=14
| a(-3,4) | » write down the given point |
| x=-3 & y=4 | » write down value of x & y |
| 2x + 5y = 14 | » write down the line |
| 2(-3) + 5(4) = 14 | » sub in the values |
| -6 + 20 = 14 | » work it out |
| 14 = 14 | » statement is true |
Since this statement is true this verifies that the point a(-3,4) is on the line L:2x + 5y = 14
![]()
Go back to the top of the page
![]()