Equation of a line

 

To find the equation of a line we need:

  1. Slope (m)

  2. One point on the line (x1,y1)

 

We can the use the following equation :

     

 

Example:

Find the equation of the line joining a(-1,3)  and b(7,5)

Step 1:    We have a point but we need the slope to find the equation.  Since we have two points we can use the formula:

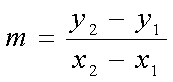
a(-1,3) b(7,5)     » write down values

(x1,y1) (x2,y2)        

    of (x1,y1) & (x2,y2)       
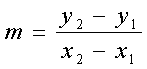
  » write out the formula
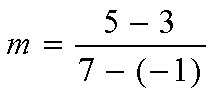» sub in the values
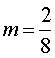
» work it out
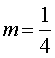
» slope

           

Step 2:     Now that we have found the slope we use this and one of the points to solve the equation.

Slope =    ¼          (x1,y1) = (-1,3)

» write out the formula
» sub in the values
» work it out 
» multiply across by 4
» work it out
» bring y & x to one side

 

Parallel and Perpendicular Lines

 

  1. Parallel       

       If two lines are parallel then their slopes must be equal

m1 = m2    

 

  1. Perpendicular

       If two lines are perpendicular then multiplying the two slopes will be equal to -1

m1 * m2 = -1

 

 Note:    If you are told in the question that two lines are perpendicular  then this means that the slope of the first line is the slope of the other inverted with the sign changed.

 

Example:

Slope of a line =   

(m1)

Any line perpendicular to this has a slope of

(m2 ) 

   m1  *   m2    = -1

         *    = -1

       

Example:

Which of the following lines are parallel and which are perpendicular?

  1. A: 3y-x=7   &  B: 6y-2x+11 

  2. C: 2y-3x=4  &  D: 3y+2x=7   

 

In order to find out which lines are parallel and which are perpendicular we need to get the slopes of both sets of lines and compare them.

 

A: 3y - x = 7  B: 6y - 2x +11 
     y =mx+c       y = mx + c
   3y = x + 7       6y = 2x + 11
    y =        y =
      m= 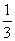                   m =

The slopes of these lines are the same therefore the lines A & B are Parallel                                            

C:2y - 3x = 4 D: 3y + 2x = 7   
     y = mx + c              y = mx + c
   2y = 3x + 4          3y = -2x + 7
     y = 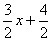                                 y =  
     y = 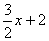                    m =
    m =   
*  = -1

If we multiply the slopes of these lines we get -1 which means that the lines C & D are Perpendicular.

 

Go back to the top of the page