Author: MathsManiac
Due to popular demand (i.e., apparently at least two people are interested!) I have decided to put together a web-based tutorial on this option, which is the least popular one on the Leaving Certificate Higher Level course, and for which there appear to be no textbooks.
| The tutorial is based on the philosophy that the most important thing in learning a new maths topic is to gain a good intuitive feel for it, following which the mechanical stuff will be easy. The webpages include java-based "dynamic geometry" diagrams - that is, diagrams that you can click on and manipulate. These are crucial for building understanding, so you do need to have a java-enabled web browser, and you need to allow the browser to run ActiveX controls. The first time your browser loads one of these, it may take a bit longer to load, as the browser has to load up the relevant "engine". During the same browsing session, subsequent diagrams will load quicker.
The example on the right is just to show you what I mean. It's just an illustration of an axial symmetry, which is a transformation you'll have met at Junior Cert. You can interact with the diagram by dragging any of the lettered points, which will help to build understanding of the concept. If you don't see a diagram to the right, but a message instead that says "Sorry, this page requires a Java-compatible web browser", then it means either that you don't have Java (in which case you need to go to www.java.com and download it) or that your browser is preventing Java applets from running, in which case you need to tell it to allow them. By the way, when I'm giving diagrams with transformations in them, I'll try to use red for the original object and green for its image under the transformation (and I'll refer to them as the "object" and "image" respectively). Note that there are occasionally some ordinary non-dynamic diagrams too. |
|
I'm assuming that you're a good self-directed learner (otherwise you wouldn't be looking at this). Some suggested exercises are interspersed throughout. When you're finished all of the material, you should be able to handle all of the past LC questions on this topic. If you get stuck, look back through this material and you should be able to find something relevant here to help you out. If you're really stuck, e-mail me and I'll try to help. (I'm fairly confident that I won't be snowed under by thousands of students clamouring for assistance on this topic.)
I'm also assuming that you've already covered the co-ordinate geometry, including the transformation geometry, on the core syllabus, although I will revisit some of that. I'm also assuming you know what a matrix is and that you can multiply them and find their inverses.
Finally, I'm also assuming that you're actually interested in this stuff, and that you accordingly won't mind when, in order to aid understanding, I mention one or two interesting things that stray slightly beyond the scope of the syllabus. Of course, I won't waste much of your time on such things!
Lest I be accused of misleading people, I want to point out that, although I taught LC Higher maths for many years, I never taught this option in class (just never got around to it - I taught the other three at different times). However, I do understand this topic pretty well myself and am familiar with the requirements of the syllabus in relation to it.
This topic doesn't strike me as any harder, easier, longer, or shorter than the other options. Accordingly, don't expect to master it with a few hours' work. Note that these options were designed to be taught over a period of about six weeks (i.e. about 30 class periods, with homework on top of that).
I want to do two things before we really get started. The first is to introduce you to the use of matrix notation for dealing with transformations. The syllabus encourages the use of this notation even for the core material, but it's not required for the core, and most teachers don't use it. It is required for the option. Even if your teacher has done it, read through this section to be sure we're on the same wavelength.
The second thing I want to do is to do a quick review of some of the core material, to make sure you really appreciate the significance of the results that were proved there, and to make sure you understand the terminology I'll be using.
On the core syllabus, you'll have seen transformations written like, for example:
We can re-write this in matrix notation as:
If you multiply out the matrix expression on the right you can see that it reads exactly the same as the first phrasing.
Here, the point (x, y) is written as the column matrix 
, usually called a "column vector" or just "vector". In the context of transformation geometry, people often use the words point and vector interchangeably, even though they're not technically the same thing. If you just think of it as the vector from the origin to the point, you'll see that there's an exact correspondence between the two, so interchanging them isn't any harm. For example, we can write the point (3, 5) as 
, (and indeed we could also write it as 
).
One of the very handy things about writing the transformation in matrix form is that the inverse transformation is just the inverse matrix. Thus, instead of trying to solve a pair of simultaneous equations to find f-1, you have the much easier task of inverting a matrix.
For example the inverse of the transformation above is
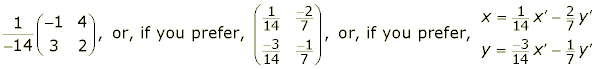
These are all just different ways of saying exactly the same thing, (and all equally valid for exam purposes).
Example:
Let f be the transformation 
. Find the image of the line 3x-2y+4=0 under f.
Solution:
Remember that to get the image of a line, you first need to invert the transformation, and then substitute in for x and y.
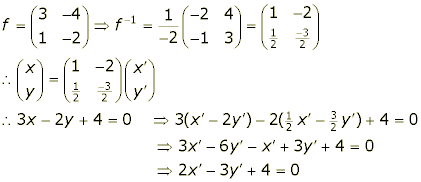
Exercise:
Take any of the questions you have done on the core transformation geometry, and re-do them using matrix notation.
Transformations that can be represented by a matrix in this way are called linear transformations. They are the only transformations that are on the core syllabus. Note that if the determinant of the matrix is 0, then the transformation has no inverse. If the determinant is not 0, we can invert the transformation. In this case, it is called an invertible linear transformation. All of the results that you had to be able to prove on the core, (such as: the image of a line is a line, the image of a line segment is a line segment, etc) related to specific invertible linear transformations.
Most students don't understand the significance of the results that are proved on the core syllabus, so I want to probe this a bit. You might be tempted to say: "So the image of a line is a line; big deal; sure what else would it be?"
Well, if you had a different kind of transformation, one that is not linear, then the image of a line might not be line at all; it might be a curve of some sort. Play around with the two dynamic sketches below. The first illustrates a transformation that is not linear. The second one is linear. In each case, you can drag the free points P, A, B, C, D and E, and observe the image point P', the image of the segment [AB] and the image of the triangle CDE. (You can't drag the image points directly (the ones with the dashes) - you can only drag the object points.)
A non-linear transformation
A linear transformation
By the way, you need to be especially careful with language when talking about non-linear transformations. For example, I couldn't refer to C'D'E' as "the image triangle", because it isn't a triangle! So, you may have noticed that I referred to the shape C'D'E' as "the image of the triangle CDE". In the non-linear case, the image of the triangle CDE is the figure C'D'E' (whose shape may be unknown), and in the linear case, the image of the triangle CDE is the triangle C'D'E'.
Important note: Non-linear transformations are not on the syllabus (core or option) so you don't have to be able to deal with them at all. I have shown the above to you because I believe that you can't really appreciate how significant it is for a transformation to have these properties if you've never seen one that doesn't.
Now that you realise that not all transformations are as well-behaved as linear ones, note that the following things are true of invertible linear transfomations and not necessarily true of other transformations:
This last property is illustrated in the following sketch. Note that [AB] and [CD] are constrained to remain parallel. None of the actual lengths are preserved under the transformation. However, the ratio of |AB| to |CD| is preserved, (meaning that the ratio of |A'B'| to |C'D'| is the same as the ratio of |AB| to |CD|), whereas the ratio of |AB| to |EF| is not preserved. (You can drag the endpoints of the red segments and the meaurements will update as you go. If you want to change the ratio of |CD| to |AB|, you have to drag C or D.) By the way, I'm not sure what the units of measurement are; I guess they're pixels or something like that.
Ratio of lengths under a linear transformation
I think it's time I went on to a new page!