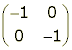
I now want to link up two things that you've already studied. In your Junior Cert geometry, you dealt with some transformations on an informal basis, using diagrams and pictures to explore how things get flipped, rotated or moved under various transformations (translation, axial symmetry, central symmetry, rotation). On the Leaving Cert core, you dealt with linear transformations in the co-ordinate plane. How are these two connected? Let's try to do some of the transformations from the Junior Cert course using the methods from the LC core.
For this, you need to do some proper hands-on practice: I want you to get out some graph paper and do the following: take any three points A, B and C, as the vertices of a triangle. For each of the transformations below, apply the given matrix to your chosen points to get the images A', B' and C'. Then show both the original triangle and its image on graph paper, so as to observe that the transformations really are doing what I'm claiming they're doing. (If you don't have any graph paper handy click here for a Microsoft Word document consisting of an A4 page of 5mm square grid paper, which you can print out.)
Central symmetry in the origin: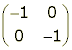
Axial symmetry in the x-axis: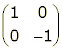 
Axial symmetry in the line x=y: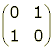 
90o anti-clockwise rotation about the origin: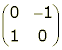 
37o (approx) anti-clockwise rotation about the origin: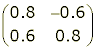 
[Aside: here's an interesting thing to consider: when you were drawing the image of triangle ABC in the above examples, did you join the image points A', B' and C' with straight line segments? How did you know that that was allowed? (i.e. that the image of the straight segment [AB] would be the straight segment [A'B'], and not some squiggly curve joining A' and B'? You were right to do so, of course, but if you can't explain why, then you weren't paying attention earlier!]
Of course, not all of the linear transformations on the core syllabus behave like the transformations that you had at Junior Cert. Sometimes they stretch or squash things out of shape, and make them bigger or smaller.
Exercise: Apply the transformation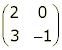 
to any triangle you like. You'll find that the image triangle is a different size and shape from the original, (although it is still a triangle).
Over and above the properties of linear transformations, all of the transformations you met on the Junior Cert syllabus had the additional property that lengths don't change. A transformation that leaves all lengths unchanged is called an isometry. Once lengths are preserved, it follows that the image of any shape will be congruent to the original shape. (Think about why this is so, or try to prove it if you can.) Isometries therefore preserve angle, shape, size and area.
As we have seen, not all linear transformations preserve length, so they are not all isometries. Axial symmetry, central symmetry, and rotation are all isometries, and we've already looked at some matrices that represent special cases of these. There is another isometry that you had at Junior Cert, and that's a translation. Unfortunately, a translation is not a linear transformation, and so cannot be represented by mutiplication by a square matrix. To see this, note that all linear transformations leave the origin fixed. (Try multiplying any square matrix by the vector representing the origin.) But a translation doesn't leave the origin fixed, so it's not linear.
"Now hold your horses, there, Maniac", I hear you say, "Didn't we see earlier that rotations and axial symmetries and central symmetries were linear? But they don't always leave the origin fixed."
Actually, I never said that all of these types of transformations were linear. I just happened to pick some special cases that were linear. The full story is this: an axial symmetry is linear only if the axis of symmetry passes through the origin, a central symmetry is only linear if the symmetry point is the origin, and a rotation is only linear if it's a rotation about the origin.
So now we have a bit of a problem. We'd like to be able to use matrix methods to deal with all of these transformations, but transformations of the form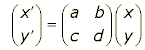 
just won't cut the mustard, so to speak. So we need to extend things a bit.
Remember that a translation just slides everything in some direction. You did translations in co-ordinate geometry for Junior Cert. Recall that all you had to do was add some fixed number to the x-value and some fixed number to the y-value. For example, if f is the translation that sends (0, 0) to (3, -2), then you find the image of any point by adding 3 to its x-value and -2 to its y-value. In matrix notation, we can write:
So, basically, you do a translation by just adding on a column matrix (i.e. vector).
Thus, if we allow this operation of adding on a fixed vector, as well as the operation of multiplying by a matrix, we can now do translations as well as linear transformations. Now our good luck kicks in: it turns out that allowing these two operations only - multiplying by a matrix and then adding on a fixed vector - we can actually do all of the transformations we are interested in. We can do axial symmetries through lines that don't go through the origin, and rotations about points other than the origin, (and of course we can continue to do stretchy, squashy things too!).
We therefore define this important new class of transformations, called affine transformations
An affine transformation is an invertible linear transformation followed by a translation. In matrix form, this is expressed as:
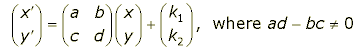
The square matrix multiplying the vector is the linear transformation part; the condition that the determinant, ad-bc, is not zero ensures that it is invertible; the addition of the "k" vector is the translation part. Since the translation part preserves everything except position, it follows that any stretching, squashing, turning, or flipping that this transformation does is done by the matrix bit - the linear transformation.
Exercise:
Take any affine transformation you like (i.e. any numbers you like for a, b, c, d, k1, k2,) and find the images of a few points, just to get the hang of applying an affine transformation.
It's worth mentioning that the translation part of the transformation is a pit of a pain. It makes it more awkward to invert the transformation. Instead of just inverting the matrix, you now have to do two steps: subtract off the translation vector first, and then apply the inverse matrix. Furthermore, if you want to write this inverse in the correct form for an affine transformation, you'll notice that the two steps are in the wrong order, so you've to do a bit of algebraic manipulation to express the inverse as a linear transformation followed by a transformation. (If you want learn about a clever way that's used to get around this issue, [not required for Leaving Cert,] see the the following part of a Wikipedia article: http://en.wikipedia.org/wiki/Transformation_matrix#Affine_transformations.)
You don't have to be able to find the matrix representation for any given affine transformation, (although there are some particular ones you need to be able to do, which we'll see when we study the ellipse later on). However, just to illustrate how a transformation of this form could represent a familiar type of transformation, try the following exercise:
Exercise:
Consider the transformation
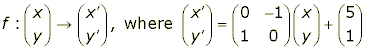
(i) There is a point P(x1,y1) that doesn't move under f. Find it. (i.e., find the point P such that f(P)=P.)
(ii) f is actually an anticlockwise rotation about P. Illustrate this by: drawing the triangle ABC where A=(5, 2), B=(6, 2) and C=(5, 4), and then finding and drawing the image of ABC under f.
This latter point is often used as part of the definition of an isometry:
Defn: An isometry is an affine transformation that preserves length.
Example/Exercise:
The following transformation is an isometry.
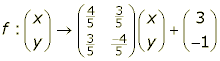
Pick any two points a and b and show that |f(a)f(b)| = |ab|. (Note that your calculations will be easier if you pick points whose co-ordinates are multiples of 5.)
Suppose you're just given an affine transformation. That is, a transformation of the form:
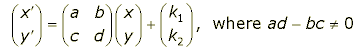
How do you figure out whether or not it is an isometry? Firstly, it's clear that the translation part (the k1 and the k2) isn't going to affect whether or not it's an isometry, since that bit will always preserve lengths. So the question is, can you tell from the values of a, b, c, and d whether this is an isometry? The answer is "yes".
I begin by making the assertion that if an affine transformation preserves the distance from the origin to any given point, then it will preserve all distances. Try to prove this yourself. (Hint, given any two points P and Q, construct a parallelogram with P, Q, and the origin as three of its corners.)
My question has now become: what conditions on a, b, c, and d will result in the distance from (0, 0) to (x, y) being preserved? Time for the donkey-work. (I'll use distances squared instead of distances, to save writing out the square roots.)
The squared distance from (0, 0) to (x, y) is x2 + y2.
Also, x' = ax + by and y' = cx + dy, so the squared distance from (0, 0) to (x', y') is (ax + by)2 + (ax + by)2.
Multiplying this out and gathering appropriately gives: (a2+c2)x2 + (b2+d2)y2 + 2(ab+cd)xy.
So, for an isometry, we want the squared distance from (0, 0) to (x, y) to be the same as the squared distance from (0, 0) to (x', y').
That is, we want x2 + y2 = (a2+c2)x2 + (b2+d2)y2 + 2(ab+cd)xy.
But remember that we want this to be true for all x and y.
This will happen if and only if the coefficients of x2, y2, and xy match on the two sides.
That is, it will happen if and only if: (1) a2+c2 = 1, (2) b2+d2 = 1, and (3) ab+cd = 0.
So, the above three conditions on a, b, c, and d are the conditions for an isometry.
Exercise: Go back and check that these three conditions hold for all of the isometries we've looked at already.
I don't think you need to know the above three conditions off by heart; I've never seen a question that requires this. But I think you probably could be asked to establish them, (i.e. more or less as above).
Also, it's probably worth pointing out that you can use the above three equations to express the matrix in terms of a single variable, and to fully classify all the possible types of isometry, as follows. (You'd hardly have to be able to reproduce the argument the follows below, but the final result is worth knowing anyway.)
First, note that the first two conditions clearly mean that all four of a, b, c, and d must be between -1 and 1 (inclusive). We could use the equations to express all four in terms of a, but instead, since a can run from -1 to 1, let's write a = cosθ. This gives (from equation (1)) c = ±sinθ. However, since there are two values of θ between 0° and 360° that give cosθ = a, we can make sure we pick the one that gives c = sinθ. We can follow the same procedure with b and d, expressing them as, say, cosΦ and, (from equation (2),) sinΦ. However, equation (3) then allows us to show that θ-Φ = 90° or 270°. (Verify this.) If it's 90°, we can write cosΦ = -sinθ and sinΦ = cosθ; whereas if it's 270°, we can write cosΦ = sinθ and sinΦ = -cosθ. Accordingly, we have established that the only two patterns of matrix that can give an isometry are ones of the form:
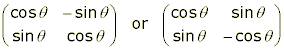
The first matrix above represents an anticlockwise rotation about the origin through θ°. The second one represents an axial symmetry (reflection) in a line through the origin making an angle of (θ/2)° with the x-axis. When these are combined with the possibility of a translation, we have the full classification of all possible plane isometries:
By the way, a reflection followed by a translation yields two possibilities: if the translation is in the direction perpendicular to the axis of symmetry, then the composite can be expressed as a single reflection (about a different axis). If it's not, then it can always be expressed as a glide reflection. (That is, if the translation is not parallel to the symmetry axis, then you can get it to be parallel by picking a different symmetry axis parallel to the original one.)
Apart from the identity, here are dynamic illustrations of the other four types. In each case, you can drag the letterd points and the corners of the red object.
|
Translation |
Rotation |
|
Reflection |
Glide reflection (intermediate step shown pale) |
Given that isometries preserve length, you should be able to satisfy yourself, using the SSS rule, that the image of a triangle is congruent to the original. Therefore, isometries will also preserve the area of a triangle. Also, since any polygon (i.e. any straight-sided shape) can be broken up into triangles, isometries preserve the areas of all such shapes. (And we could extend this to curved shapes by thinking of approximating the shape with a many-sided polygon.)
One last thing that might be worth mentioning is the idea of "orientation" or "handedness". Imagine you label the vertices of a triangle ABC so that going from A to B to C is clockwise. You'll find that in the image of this triangle under a translation or rotation, they are still clockwise, whereas under a reflection or a glide reflection they flip over to anti-clockwise. We say that the image has the same or opposite orientation as the original object, (or same/opposite handedness: imagine a picture of a right hand and think about whether it stays a right hand or becomes a left hand under the different types of isometry).
Also, every isometry can be expressed as a product of at most three reflections. (Composition of two reflections in parallel lines is a translation and in two non-parallel lines is a rotation about their point of intersection. A glide reflection, being a reflection followed by a translation, is therefore a product of three reflections.) Since a reflection flips the orientation, then an isometry that's a product of an even number of reflections (i.e. two) preserves orientation.
We've certainly covered the course requirements in relation to isometries very well here, but if you want to read further, see the Wikipedia page about this stuff: http://en.wikipedia.org/wiki/Euclidean_plane_isometry. In particular, if you're also lucky enough to have studied the "Groups" option, it develops this aspect (the plane isometries form a group under composition), and you'll find it interesting too to follow the further links to stuff about "wallpaper groups", "frieze groups", "crystallographic groups" and "crystallography".