The latin word locus (plural: loci) means "place". In maths, it's used in phrases such as "The locus of a point which..." The locus of a point satisfying a particular property is the "place" where such a point is or could be. You might prefer to think of it as the set of all places where the point could be, or simply the set of all points satisfying the property. Loci are often described using language that refers to motion. For example, instead of saying "The locus of the point such that property X holds", we might say "The locus of a point that moves in such a way that property X holds". Accordingly, a locus is often though of as the path traced out by a moving point that is constrained in some way.
|
For example, given any two points A and B, determine the locus of the point P that moves in such a way that its distance from A is always equal to its distance from B. The diagram on the right shows this scenario. The diagram has been constructed in such a way that P is constrained to always satisfy the given condition, even though you can still drag it. Also, to assist you in visualising the path that it traces out, I have set it up to leave a trail or "trace" behind it as it moves. There will be more diagrams later with such traces in them. Whenever you activate these, a little red "x" appears in the bottom right of the diagram. Clicking on this x clears the trace, so you can start again. Drag P now, before you read on. Then clear the trace, move A and B, and drag P again. You should get a pretty clear picture of the path being traced out. |
|
So, I hope you figured out that the path traced out by P is the perpendicular bisector of [AB]. Indeed, you may have been reminded that in Junior Cert geometry, you encountered the fact that every point on the bisector of a line segment is equidistant from the ends of the segment. That's clearly what's going on here.
You can of course work with loci in co-ordinate geometry. It is often possible to use the definition of the particular locus in question in order to find the equation of the locus. For example, in the above case, suppose that A is the point (1, 6) and B is the point (5, -2). If P(x, y) is any point satisfying the given constraint, you can write this as an equation in x and y as follows:
![]()
Exercise:
Simplify the above equation to show that it's the equation of a line. Draw it, along with A and B, on a co-ordinate diagram to satisfy yourself that it is the perpendicular bisector. Prove that it's the perpendicular bisector, by verifying that it is perpendicular and that the midpoint of [AB] is on it.
Another example of a locus that you've already met is the circle. The circle can be though of as the locus of a point moving in such a way that its distance from a fixed given point (the centre) is always equal to a fixed given number (the radius).
|
There are a few different ways to define an ellipse, but the usual one, and one that is used on the Leaving Certificate course, is as follows: Given any point F (which we will call the focus)and any line l (which we will call the directrix, consider a point P whose distance from the focus is some fixed multiple e of its distance from the directrix, where 0 < e < 1. The locus of the point P is called an ellipse. The locus is shown in the illustration on the right. You can drag the focus, F, and drag A and B to change the directrix. You can also drag the point e on the slider from 0 to 1 to change the eccentricity. The closer e is to 0, the more circular the ellipse is. If you want to see how a point P generates the locus, click the indicated button to show P and also its distance from F and from the directrix AB. |
|
Just as it is possible to get the general equation of a circle in any position in the co-ordinated plane, so also is it possible to get the equation of an ellipse in general position. However, the algebra involved in dealing with an ellipse in general position is very awkward, so instead we choose a co-ordinate system so as to leave the ellipse in a "nice" position. After all, the co-ordinate axes are just a pair of perpendicular lines like any other such pair, so we might as well pick a pair that suits us. (In particular, we're going to choose axes in such a way that the ellipse turns out to be symmetric about both the x-axis and the y-axis.)
|
Some of the following paragraph consists of pulling things out of the blue a bit, but you don't need to remember the details of it. All you really need to know is the paragraph after it! We start by taking the line through the focus that is perpendicular to the directrix, and make that the x-axis. Next, we need to pick a point along that line to be the origin; that will then serve to fix the y-axis (which obviously has to be perpendicular to the x-axis). Looking at our locus, it appears to have a "centre", which we would like to make the origin, except that we don't really know where that it is in relation to the focus and the directrix. It turns out that everything works out fine if we choose the origin as follows: Let d be the distance from the focus to the directrix. Then take the origin to be the point on the x-axis whose distance from the directrix is d/(1-e2), and which is on the same side of the directrix as the focus. If we then let a be the number ed/(1-e2), we end up with the following, which you can verify if the mood takes you: We have created a co-ordinate system such that the focus is at the point (0, ae) and the directrix is the "vertical" line x=a/e. Needless to say, we usually "turn the page around" so as to make the axes horizontal and vertical! |
|
So, can we find the equation of the ellipse with this focus and directrix? Remember that to find the equation of a locus, we express the defining condition as an equation in x and y. In this case we have:
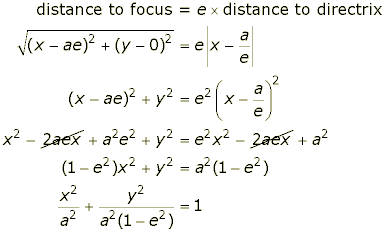
Now let b be the positive quantity defined by b2=a2(1-e2). Then we have:
![]()
What can we now say about this curve? You should be able to satisfy yourself as to the following:
Thus, the following diagram describes the situation:
Co-ordinates of important points related to the ellipse
When the co-ordinate system has been chosen as we have done, the ellipse is said to be in standard position. You should make sure that you know the co-ordinates given on the above diagram. That is, the locations of the foci, the directrices and the intercepts of the ellipse in standard position.
Given that we have established central symmetry about the origin, we refer to this point as the centre of the ellipse.
Any line segment whose endpoints are on the ellipse is called a chord of the ellipse.
Any chord that passes through the centre of the ellipse is called a diameter of the ellipse.
The longest diameter of the ellipse is called the major axis. When the ellipse is in standard position, this is along the x-axis. The quantity a, (which is half the length of the major axis) is called the semimajor axis.
The shortest diameter of the ellipse is called the minor axis. When the ellipse is in standard position, this is along the y-axis. The quantity b, (which is half the length of the minor axis) is called the semiminor axis.
A line that intersects with the ellipse in one point only is called a tangent to the ellipse.
Note the equation that we had during the last derivation: b2=a2(1-e2). This allows us to find the eccentricity if we are given the semi-major and semi-minor axes, or to find one ot other of the semi- axes, given the other one and the eccentricity.
Example: Find the equation of the ellipse in standard position, with eccentricity 1/2, whose major axis is 10 units long.
Solution: a=5 and e=1/2 gives:
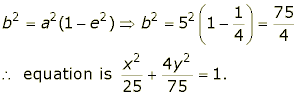
Note that it is usual to give the equation of an ellipse with a 1 on the right-hand side - we don't multiply across here to clear the fractions. The reason is that in this form, it's easier to read off the semi-major and semi-minor axes.
Another example: Find the eccentricity of the ellipse whose equation is 4x2+9y2=25.
Solution: First express in friendlier format, by dividing across to get the right-hand side equal to 1:
![]()
This tells us that a=5/2 and b=5/3. From this, we get:
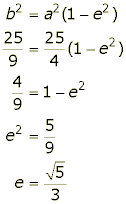
Another example: Find the equation of the ellipse in standard position which has eccentricity 0.9 and a directrix at x=3.
Solution: Directrix is at x=a/e. Hence, a/e=3, so (0.9)a=3, so x=10/3, and finish as first example.