<< Previous page Next page >>
An Interesting Property of the Ellipse
Most of the things we're going to prove about an ellipse will be established using transformation geometry, but here's one thing that's easier to do in a more straightforward way:
If p is any point on an ellipse, then the sum of the distances from p to each of the foci is constant. (In fact, it's always equal to 2a.)
Exercise: Prove the above statement, using the defining property of the ellipse.
|
This fact gives another means of constructing the ellipse. Instead of using the focus-directrix definition of the ellipse, We could have defined it as the locus of a point P moving in such a way that the sum of its distances from two fixed points F1 and F2 is a constant. This gives a practical means of drawing an ellipse, which is often used in reality if trying to draw a very large one, such as for building or laying out an elliptical flowerbed: place two pins or stakes at the two foci; then tie a string to the two pins, leaving enough slack so that the string's total length is 2a; hold the pencil or drawing implement against the string, keeping it taught, and move it around to draw the ellipse. It's a bit easier in practice if you make a loop around the two pins, extending the string appropriately. Here's a link to a description with photos of someone using this technique on a piece of wood: http://www.instructables.com/id/Drawing-Ellipses/, and here's a you-tube video: http://www.youtube.com/watch?v=CaokHrXP8HM.
|
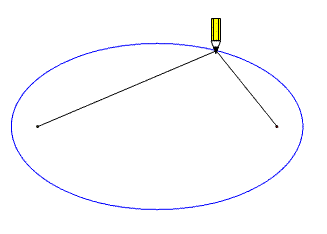
Drawing an ellipse
|
Proving things about ellipses
We will shortly be bringing together the work we did on transformations with the work we've been doing on the ellipse. Before we start this, however, it's worth pointing out that proving things about ellipses is trickier than proving similar things about circles. For example, consider the two diagrams below. The first shows a circle with a diameter, and with tangents drawn at the endpoints. The second shows an ellipse with the same thing. In both cases, it appears that the tangents are parallel. But can you prove this? In the first case, there's a Junior Cert theorem to help you: the tangent to a circle is perpendicular to the diameter at the point of contact. This makes it easy to prove parallelism in the first case. Unfortunately, the tangent to an ellipse is not, in general, perpendicular to the diameter at the point of contact. So, the same proof doesn't apply.
|
Tangents at the ends of a diameter of an circle
|
Tangents at the ends of a diameter of an ellipse
|
Before continuing, try to prove the parallelism in the second case (but don't be surprised if you can't!)
Proof using transformations
We will set about proving the above result using transformation geometry, and this will indicate the general technique used for other proofs later. The idea is to note the result that we have for the circle, and then apply an affine transformation to turn the circle into our ellipse. Then, any property that is expressed only in terms of things that are affine invariant, will still hold true.
The first step is to produce a transformation that maps the unit circle to our ellipse. We note the following:
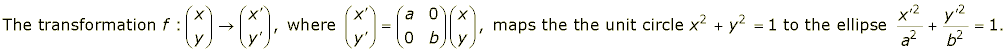
|
(Exercise: Prove the above.)
Now, suppose we have an ellipse E with equation
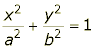
and a diameter D of the ellipse, and tangents T and S at the endpoints of D.
Then f-1(E) is the unit circle centred at the origin: x2+y2=1, f-1(D) is a line segment whose endpoints are on the circle and which passes through the centre (i.e., a diameter of the circle), and f-1(S) and f-1(T) are tangents to the circle (since tangency is an affine invariant) at the endpoints of that diameter.
Hence, f-1(S) and f-1(T) are parallel.
But parallelism in an affine invariant. Therefore, S and T are parallel.
|

|
So, there you have it. That's the technique we're going to apply to all of the results we're asked to prove about an ellipse.
Note that we have used both f and f-1 in our proof. It doesn't really matter which way around we make f. That is, we could have made f the transformation that sends the ellipse to the unit circle, in which case f-1 would send the circle to the ellipse. Either of these is equally correct, so choose whichever you wish. Remember, however, to be consistent throughout your proof.
Bisecting chords
Here's a thing that's true about circles but not about ellipses, (there was a theorem about it on the Junior Cert course): A diameter drawn perpendicular to a chord of a circle bisects the chord.
(Exercise: Remind yourself of the proof of that - it uses congruent triangles.)
Here's a dynamic illustration. (Points P, B, Q and D are dragable.)
Diameter bisects perpendicular chord in circle, but not in ellipse.
If you drag D up and down the diameter of the ellipse above, you will see that you are generating a whole set of parallel chords. Unlike in the circle, the perpendicular diameter does not bisect them. However, there is a different diameter in the ellipse that does bisect them.
Before we prove this, we will illustrate it with another dynamic diagram. In the following sketch, the point P can be dragged across the diagram, and the line it is on will move with it, while always remaining parallel to CD. As the line traverses the ellipse, its midpoint will be traced.
All the lettered points can be dragged. However, if you move points other than P, you should clear the trace before dragging P again.
What you should see above is that the green midpoint traces out a diameter of the ellipse. That is, the locus of midpoints of parallel chords of an ellipse is a diameter of the ellipse.
Looking at this the other way around is the handiest way to prove it. That is, can we demonstrate that there is a diameter that bisects all of those chords? We do this with the following result:
If D is a diameter of an ellipse, and if it bisects any chord that is not another diameter, then it will bisect all of the chords parallel to that one.
Exercise: Prove the above result, using a transformation to the unit circle. (Hint: after transforming to the unit circle, show that the image-diameter is perpendicular to the image-chord.) (Another hint: if you find the idea of "all other chords" too tricky to deal with, rephrase as follows: Given a diameter D of an ellipse and two parallel chords that are not diameters, prove that if D bisects one of them then it will bisect the other.)
Conjugate Diameters
Looking back at the last sketch again, note that among all of the chords generated by dragging P, one of them is itself a diameter. In other words, we could rephrase what happened in that sketch as: The locus of midpoints of chords parallel to a given diameter is another diameter. This gives a connection between two diameters of an ellipse. The second diameter is said to be conjugate to the first. As it happens, this relationship is mutual: that is, the first diameter is also conjugate to the second. This is established by the following result:
If a diameter D1 of an ellipse bisects all of the chords parallel to another diameter D2, than D2 bisects all of the chords parallel to D1.
Exercise: Prove the above result, using a transformation to the unit circle.
<< Previous page Next page >>