CHESMAYNE
![]()
Knights
The KT puzzle where the KT lands on every cell only
once are called “The
KTs
Tour”. At the following link you
will find an animated Tour and another link to a website with several different

http://www.chess-poster.com/english/chesmayne/the_knight.htm
Puzzle.
The KT is moved on 64 occasions, entering each cell only once during this
tour. The solution is called
‘re-entrant’ if the KT finishes in a cell which is a KTs move away from the
starting cell. The other knights of Chesmayne may
be used in the same manner (KN, SB, KM etc). The number of possible KT tours is 122+
million.
Could
you do the ‘KTs Tour’ in three minutes in front an audience of millions? That is exactly what Paul Broad from

In
a KTs Tour the Knight must travel to every square/cell on the board without entering any cell more than once while moving in
an L-shape as it normally would in a game of chess. There are many ways of
achieving this. The example which
follows shows one variation. The KT starts on the cell numbered one and travels
to each cell in numerical order, finishing on cell 64.
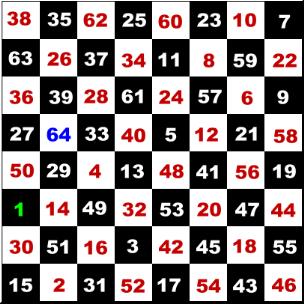
A Knights Tour
“Knight’s Tour” is a puzzle which has amused chess players throughout the ages. The goal of the KT is to traverse around the board, landing on each cell but once. There are numerous solutions. Here’s one – with an animation…….
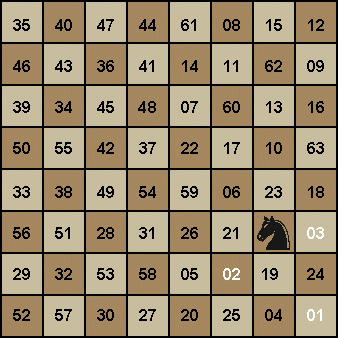
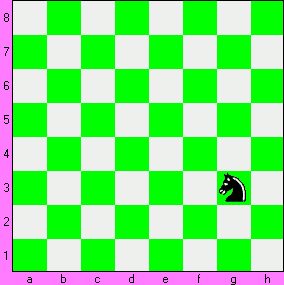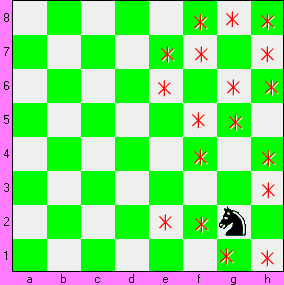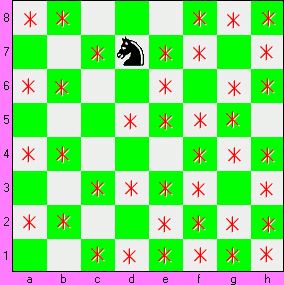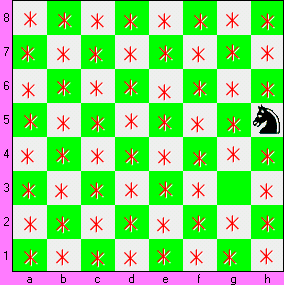
Here’s another one:
The above two
paths are known as ‘closed’ or ‘re-entrant’ paths. The KT, after completing its journey, lands
on the 64th cell, which is also the cell that it started on. Thus, it can complete the journey
again.
This is
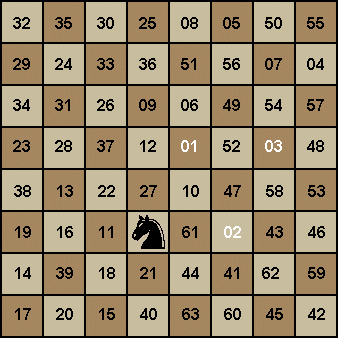
considered much more of an elegant solution than the many “open” paths, one of
which is shown here:
As you can
see, the KT still lands on each of the 64 cells. However, he isn’t able to complete the
journey a second time. In this tour,
the KT starts out here on the h8 cell, but ends up on c6... more than a KTs
move away.
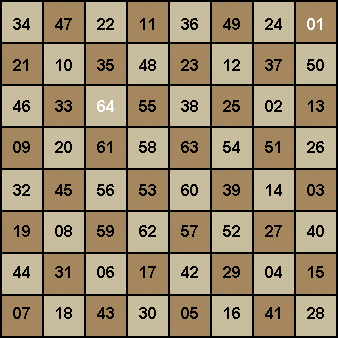
Not only is
this next example a ‘re-entrant’ path, but it’s considered a somewhat semi magic square. Each of the columns, add up to 260!
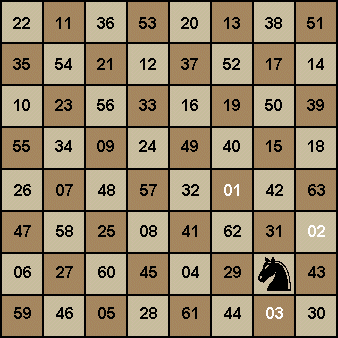
However, this one must be considered a “SUPER” magic
square which may have been created by the mathematician Leonhard Euler.
01 Each column
adds up to 260!
02
Each row also adds up to 260!
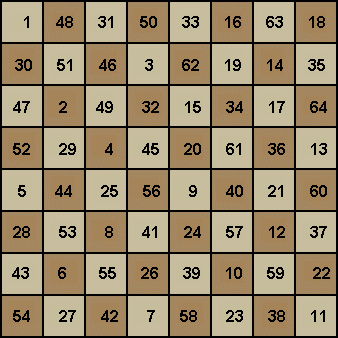
HOW MANY SOLUTIONS ARE THERE?
I.A. Horowitz
and P. L. Rothenberg have stated:
“The number of
possible ‘KTs
|
|
The KTs Tour |
|
The “KTs Tour” is an ancient puzzle in which the object is to move a KT,
starting from any cell on a chessboard, to every other cell, landing on each
cell only once. This is usually
considered to be a very challenging puzzle, so the discovery of the solution
described below came as quite a surprise!
To learn more about KT Tours, explore the links below (and watch for new
additions to this site in the near future).
|
|
The Knight's
Tour -- An Extremely Simple Solution Semi-Magic
Square Knight Tours Closed
(Reentrant) Knight Tours |
This
site is sponsored by Borders
Chess Club

KTs Tour Art
The following Knight’s Tour reflects simplicity, beauty, and
semi-symmetry in which the two left quadrants show the same path of the KT,
while the two right quadrants mirror the path.
Please contact me if you have created interesting KT tours. I will pick the best ones and add them to
this section of the webpage.
Click on the image above for a static view
Another interesting tour gem, a mini-KT tour of only 16 moves, can be
used to create the most amazing geometric pattern called a 4th
dimensional hypercube. The path of the
KT could be: d8, b7, a5, b3, d2, f3, g5, f7, d6, c4, e5, c6, d4, e6, c5,
e4. By placing a dot in the center of
each cell that the KT moves to, then connecting each dot with a line that
represents a legal KT move, the end result is a perfect 4th
dimensional hypercube. Notice that there
are 16 different cubes, all of which have the same exact dimensions, inside the
hypercube. Can you find them?
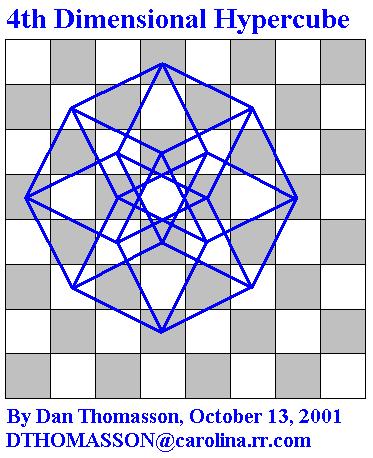
Below you will find an interesting pattern that can be
repeated over and over again to make larger and larger closed KT tours. The pattern comes from my ‘Closed KTs
Solution Key’. Ceramic tiles, wood, or
plastic can be cut into these basic shapes to make the secret closed KTs tour
pattern. The cut pieces could then be
put on floors, walls, or table-tops.
For simplicity, create the pattern for an 8 x 8 square board. Do not put numbers on the top of the
pieces. If you want to make it into a
puzzle, cut out the pieces and put the corresponding numbers on the back of the
pieces in a very light shade or impression.
When I practice creating KT tours on paper with checkerboard squares, I
can quickly complete an 8 x 8 square closed KTs tour in 15 seconds by marking
off each KT move on the squares with the following symbols: /, -, \, |. I first
use ‘/’ for all diamond shape patterns leaning in the same direction as ‘/’ in
all four quadrants. I then use ‘-‘ for
square shape patterns in all four quadrants, then ‘\’ for the opposite diamond
patterns, and finally ‘|’ for the opposite square patterns.

After doing
hundreds, possibly thousands of KT tours, using those four simple marks (which by
the way are much easier to jot down with a pencil than numbers - especially if
the tour is 10,816 squares), I realized that they made a neat pattern on the
chessboard which could be reproduced with tiles. I just follow the path pattern that I use
for the ‘Closed KTs Tour Solution Key’ and other tours that are displayed on
the KT Tours web page.
I might consider making a cool poster out of it or some of the other
tours I’ve created. There is a definite
symmetrical pattern. Just think, by
creating that one quadrant, it can be used as computer wallpaper, web page
background, watermarks, or quilts by tiling it. Experiment by changing the line colour and
thickness, and the tile colour. By
combining these four shapes in various ways, alphabets, number systems, and
ciphers can be easily created. Who
knows, maybe there could be a fictional story written that centers its plot
around the patterns in the ‘Secret Closed KTs Tour’.

[Intro] [Simple Solution] [Semi-Magic Square Knight Tours]
[Closed Knight Tours] [Solving with Number Pairs]
[Knight Tour Cube] [Knight Tour Tessellations] [Links to Knight Tours]
www.BordersChess.org/KTart.htm modified 2002.03.06
The KTs Tour
An
Extremely Simple Solution
I would like to share a KTs Tour I created by using a very simple rule I
devised that requires no memorization: Start at any
corner and continuously rotate in the same direction around the board moving on
the outermost squares. The moves
create a semi-symmetrical pattern around the board. The tour is completed with only four trips
around the board. Feel free to post this
solution on your web-pages, other publications, or with other KT Tour
enthusiasts. Please reference my name
and e-mail address when posting my design and KTs Tour solution.
|
|
|
I originally created the chessboard in Excel which I could also use to
automatically sum the rows, columns, and diagonals. My KTs Tour does not reflect a ‘Magic Square’ but does provide
an extremely simple solution. I
recreated the board in Visio and added the red lines to show the symmetry. Connecting the sequential moves is fun to do
with other KT Tours, Magic Squares, and Magic Cubes to come up with different
designs.
In addition to being fun, the KTs Tour puzzle also helps chess students
to develop their ability to visualize tricky KT move sequences. The Greater
Reader
Feedback on Thomasson's Knight's Tour Solution
[Intro]
[Semi-Magic
Square Knight Tours]
[Knight's Tour
Art] [Closed Knight Tours] [Solving with
Number Pairs]
[Knight Tour
Cube] [Knight
Tour Tessellations] [Links to Knight Tours]
www.BordersChess.org/KTsimple.htm modified 2002.03.06
Closed (Reentrant) KT Tours
In the early 1940s, GM
George Koltanowski toured the countryside providing KTs tour demonstrations at
various chess clubs and tournament
events.

Grandmaster George Koltanowski, 1903-2000
copyright(C) 2000, San Francisco
Chronicle
He used a closed (re-entrant) KTs Tour for his solutions. “Closed” means that the KT moves to all
cells on the chessboard making legal KT moves and
covering every cell only once in which the last move can connect back to the
starting position (64 connects back to 1).
This is also known as “reentrant”.
A member of the audience would ask him to block out a cell on an 8 x 8
chessboard. He would begin making his
KT moves from that cell and then return to that cell with his last move.
Here is my thought process
for creating a closed KT tour.
When I create a tour, I
think of diamond and square patterns and the letters U and C.

I
divide the board into four quadrants, start with the
top left quadrant, then place the diamonds and squares in their respective
quadrants following the directional patterns of the letters U and C.
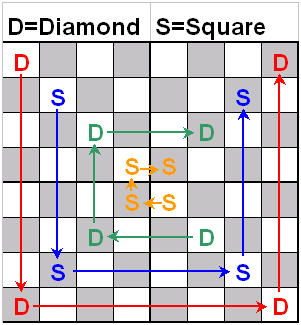
Check out the following
steps:
Step 1: I create the same
diamond pattern in all four quadrants using the directional pattern of the
Step 2: I repeat step 1, but
instead of diamonds, I create the same square pattern in all four quadrants.
Step 3: I create the same
diamond pattern in all four quadrants using the directional pattern of the
letter C.
Step 4: I repeat step 3, but
instead of diamonds, I create the same square pattern in all four quadrants.
click on the image above to see an elaborated version
Look at the closed KTs Tour below where I alternate the diamond and
square pattern for each quadrant. The
result is the same - a completed closed KT tour. What once seemed impossible to do without
the aid of a computer
is now possible and extremely simple.
click on the image above to see an elaborated version
The figure below shows a closed KTs Tour on a 16 x 16 cell board. The pattern used in this example is the same
pattern or solution that I use on boards with 1024, 4096, or even 10816 cells. For speed and ease of completing such large
tours, it is best to use the same closed tour in the 16 x 16 board that I’ve
provided, but begin the tour from the top left cell. In other words, make square 190 = 1, 191 =
2, 192 = 3, ... etc., all the way around the board until the tour is
completed. You will see just how easy
it really is!

I created the pattern in this solution key which I used to solve the 16
x 16 board KTs Tour, and it can be used on larger boards such as 32 x 32 cells,
64 x 64 cells, 104 x 104 cells, along with other board sizes.
|
|
|
Closed Knight's Tour Solution Key |
[Intro]
[Simple
Solution] [Semi-Magic Square Knight Tours]
[Knight's Tour
Art] [Solving
with Number Pairs]
[Knight Tour
Cube] [Knight
Tour Tessellations] [Links to Knight Tours]
www.BordersChess.org/KTclosed.htm modified 2002.03.06
Link to: KTs tour program
This WWW page is for a shareware MS-DOS program that solves the KTs Tour
puzzle (visit all 64 cells/squares with one KT). The small program (50k) can be downloaded
from this site. While the author of this
site doesn’t mention it, it is nice to know that the KTs tour puzzle is more
than 1,000 years old.
§
http://www.gfcs.demon.co.uk/tour/ KTs tour program.
§
From: ‘Chess Variants’ web
page.
Worse than Worthless
By Ralph Betza
Something that
is worthless has zero value. What could
be worse?
Negative Money
My dentist told me the fee for today’s visit was zero, and he hoped I
had that amount with me. Ha ha.
I immediately went into an uncommunicative reverie, thinking about
negative-valued money. If I owe you ten
dollars, you can give me a minus-ten dollar bill.
There would need to be severe penalties against destroying or discarding
or even hiding negative money, to prevent its abuse. Imagine the anti-miser, who lives well
beyond his apparent means and after death is discovered to have a huge stash of
negative money hidden in a mattress.
Strangely enough, negative money has some positive value. If you have a debt, you pay interest on it,
but if you have negative cash, it is like having an interest-free loan.
Therefore negative money would be somewhat sought after, as people would try to
keep all their liabilities in uncash.
Counterfeit negative money
would not be a problem.
The Negative Relay Knight
In the mid 1970s, I did an article for NOST-algia in which I
explored “all possible” variants of Relay Chess. One such variant allows only your opponent
to benefit from the relay powers.
Consider a piece that moves as a KT but has no capturing powers;
instead, any enemy piece a KTs move away from it gains temporarily the power of
moving or capturing as a KT. This is a
piece of negative value!
Following Mannis Charosh’s rules, the enemy KI cannot benefit from the
relay power, and the enemy PAs cannot use this power to move to their first or
eighth ranks. However, I will break
from the Charosh tradition and allow the Negative Relay KT to give an enemy
Negative Relay KT the temporary power to move or capture as KT, and my reason
for doing so is that I have seen that the resulting tactics are piquant and
charming.
Using the above rules, and replacing each side’s KTs with Negative Relay
KTs, we get a simple game called Negative Relay Chess. Here is a sample opening:
1. NegRelayNb1-c3 d7-d5 2. NegRelayNc3-e4 e7-e5 3. NegRelayN e4-f6+
NegRelayNg8-h6 4. NegRelayNf6-g8; and White has succeeded in
burying his negative-valued piece deep in enemy territory where it blocks enemy
moves and where the benefits the foe gains from it are less dangerous (but
where the opponent is more likely to be able to get pieces in range of
it). This is a strategy that might be
worthless or worse, and to achieve it W has lost several tempi.
Meanwhile, the pieces at h6 and g8 temporarily give each other the
ability to capture. Notice that the Negative Relay KT can be captured, but can
be used as though it were uncapturable because, due to its negative value,
capturing it is usually undesirable.
The move 3.Ne4-f6+ tries
to force the capture of the liability.
Instead, Black’s reply 3...Ng8-h6
provides an illustration of the temporary nature of the relay power. The sample game is very short, but provides
insight into the rules, the strategy, and the tactics; I think it’s a pretty
good sample game!
There is absolutely no doubt that one can play Negative KT Relay Chess
with Different Armies. Beware confusion and
danger of illegal moves when negative KT and negative Fibnif
mutually attack.
What’s it Worth?
The Negative Relay KT has some small potential positive value, because
it could be used to blockade a passed PA or to make tempo moves in the late
endgame. In fact, in the late endgame,
because there are so few enemy pieces to be helped by it, it might even have a
very small positive value overall.
Its whole-game value can be estimated as the amount of average mobility
it gives to the enemy times the chance that it does so, and the chance that it
does so is its own average mobility times half the probability that a random
CELL is occupied. That’s -4.59375, and
since the KTs positive average mobility is 5.25, replacing a KT with a Negative
Relay KT makes your army weaker by 9.8, or one and seven-eighths of a KT; in
other words, replacing a pair of KTs with Negative Relay KTs should
theoretically make your army 11.25 PAs weaker!
Because the KT starts at g1 and b1, where its friendly PAs shield it
from undesired contact with enemy pieces, an army that has 3.75 KTs’ worth of
power distributed among its other pieces might be able to simply win with its
other pieces while leaving its negative-valued KTs at home, right? The positive value of having a worse than
worthless piece in your army is that you get to have so much power added to
your other pieces!
Maybe not. With the funny
material balance, the levelling
effect will hurt the pieces that have added powers - for example if you
have Cardinals instead of BSs, the enemy BSs gain the ability to chase your
Cardinals away.
In order to keep the strategy of keeping the negatives at home from
being too strong, I’m going to avoid giving jumping moves as enhancements to
any of the pieces. This means that the
negative pieces, if left at home, will have the added liability of being in the
way of smooth development. Also,
because the army with negative pieces has to move PAs to develop, it must break
up the PA formation that shields the liabilities from contact with the foe.
Let’s let the RO have the additional power of moving as a three-cell
limited BS (that is, as a BS3 that can’t move farther than from a1 to d4), and
the BS also move as RO2 (making normal BS moves or short RO moves, for example
f1 to f3 but no further).
I haven’t worked out the exact arithmetic of that, but it’s close enough
to be worth a try. It feels right,
too. But omigosh, what an experimental
army, how exotic it is, and oh, so great a chance that it is too weak or too
strong! My brain is tired and I can’t
playtest it blindfold; but it’s such an exciting idea, and such a crazy army, I
can’t resist publishing it as is, just eight hours after the dentist’s joke,
with apologies if it needs to be corrected later.
The Nattering Nabobs of Negativity
The Nattering Nabobs of
Negativity[1] are a highly experimantal and untested army intended to fit into
the framework of Chess with
Different Armies.
The QU, KI, and PAs are the
normal FIDE Q, K, and P.
The R is the FIDE Rook plus short
bishop of length 3 - RB3 - and because it ought to have a name I’ll call it a Rhubarb.
The B is the FIDE Bishop
plus short Rook of length 2 - R2B -- Rutabaga is
its name.
The KT is a Negative Relay
KT, as described previously in this document.
It’s called the Ruthven,
named after the Murgatroyd whose family curse made his title of nobility worse
than worthless.
Strangenesses
I don’t have the energy to
discuss the following ideas in complete detail.
Asymmetrical Relay
“Its whole-game value can be
estimated as the amount of average mobility it gives to the enemy times the
chance that it does so, and the chance that it does so is its own average
mobility times half the probability that a random cell is occupied”. Perhaps you can detect that my particular way
of phrasing that statement encompasses the possibility of a piece moving as KT,
and granting any piece a KIs move away from it the right to move as a RO or to
capture as a BS?
Promiscuous Negative Relay
Notice that friendly pieces are not affected by the relay power of a
friendly piece. Unfortunately, the opening position is so crowded that if a
friendly PA a KTs move away from a friendly KT gained the liability of being
used by the enemy to move or capture as a KT, chaos might ensue. However, since PAs may not move to their own
first rank, the game might be playable?
But if Pd2 captures Bf1 and Bf1 is also a liability, then the capture
would be undesirable.
Therefore a game in which all pieces (except perhaps KI) are negative
relay pieces both to friend and foe might be playable after all!
Huge Negative Values
“Its whole-game value can be
estimated as the amount of average mobility it gives to the enemy times the
chance that it does so, and the chance that it does so is its own average
mobility times half the probability that a random cell is occupied”. For a symmetrical relay piece, that is, in
the natural case where the power of movement is the same as the power granted,
the negative value varies as the square of the average mobility of the
power. In other words, the negative
relay Amazon would have in theory sixteen times the negative value of the
negative relay KT! Sixteen times!
That’s more negative value in one piece than the positive value of an
entire normal army of pieces!
[1] Phrase coined by William Safire for a speech by
Spiro T. Agnew.
Written by Ralph Betza.
The Distribution of the KT

The Knight’s
Tour problem can be stated as follows…….
·
Given a chessboard with n x
m cells, find a path for the KT that visits every cell exactly once.
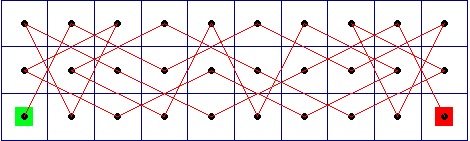
For example, here is a solution to the KTs tour problem on a 3 x 10
chess board. In this example, the KT
starts out in the lower left corner and ends in the bottom right corner:
If we started on the second square
on the first row, would it still be possible to find a solution? More generally, what does the distribution
of solutions across the chessboard look like?
That is, for every given starting point, how many solutions exist?
This problem can be solved by
computer: for every given starting point, evaluate every possible path that
visits each square exactly once, and then count how many solutions exist. We used Mathematica to do this hunt…….
We present here the
distribution of solutions across a chessboard, for all chess boards with 32 or
less cells.
Select a chessboard from the menu on the left.
Related Links
·
Arnd
Roth's page - an improvement to Warnsdorff’s algorithm.
·
Combinatorial Object
Server - the KTs tour and sequences.
·
Schröer
and Wegener's paper - (a GZipped postscript file): section 7 derives the
(currently) smallest known upper bound on the number of solutions on a 8 x 8
board: the bound is 2.544 * 1017.
·
Chess on Stamps - KTs, chess, and more.
Leapers
Chess
KTs and the like
 I intend to place a
leaper-tour solving applet at this location. For now, here is a small
article I wrote. I intended to expand this into my Master’s Thesis, but Donald Knuth wrote an
excellent article about leapers that made any expansion a moot point. In February 1956, M Apsimon posed the
question: how many cyclically symmetric KT tours on a board 10 x 10? In the 1970’s, W H Cozens reiterated the
question in ‘The Mathematical Gazette’, and published the tours below. More recently, Donald Knuth found
that exactly 2,432,932 KTs tours are unchanged by 180-degree rotation of the
chessboard. It seems the problem
from 1956 might now be answerable.
I intend to place a
leaper-tour solving applet at this location. For now, here is a small
article I wrote. I intended to expand this into my Master’s Thesis, but Donald Knuth wrote an
excellent article about leapers that made any expansion a moot point. In February 1956, M Apsimon posed the
question: how many cyclically symmetric KT tours on a board 10 x 10? In the 1970’s, W H Cozens reiterated the
question in ‘The Mathematical Gazette’, and published the tours below. More recently, Donald Knuth found
that exactly 2,432,932 KTs tours are unchanged by 180-degree rotation of the
chessboard. It seems the problem
from 1956 might now be answerable.

1956 question - how many of these are there?
Patent 694038 (1902) by W E
Stubbs patented a KTs tour on a 6 x 6 board. See GP Jelliss's page for the
history of this problem. The Stubbs
puzzle used a pegboard and pegs joined with cord. To solve the puzzle, all the lengths of cord
between the pegs had to be taut.
Suppose that you had a 5 x 5 grid of pegs. Some holes are already filled,
perhaps. With 15-25 pegs, is there
a series of lengths so that the pegs can only be put away tautly in a unique
way?
In the March 1973 issue of Games and Puzzles, Robin Merson found a
non-crossing KTs tour on an 11 x 11 board with a length of 74 moves. He found a longer non-crossing tour on a
board with a smaller area. Can you
find it?
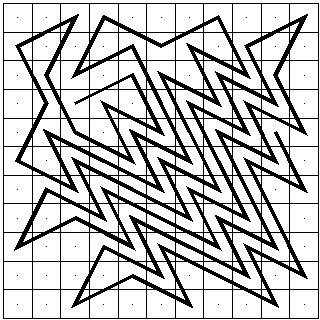
Roger Phillips has found a
smaller board with a longer uncrossing tour. A 10 x 12 board allows for a
length 75 tour. I’ve moved the
material from a few weeks ago to the Leapers page.
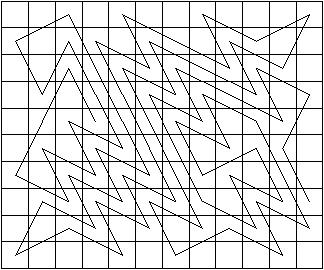
Juha Saukkola wondered what
the longest possible Knightrider
tour might be. A knightrider moves like a KT, by may keep going in a
straight line. Here is his
answer. What is the fewest number
of moves for a knightrider to tour the chessboard?

Advanced Computing Technology has a
program that solves large Leaper problems.
Keyed Tours. Each path starts at the top left corner, and starts cycling
through the KEY over and over again.
It will always take the direction suggested by the key IF a
complete closed tour would still be possible. There are three parts to the key.
1. A direction
key. Below, a simple 1=N 2=E 3=S 4=W is used. The eight paths of a knight could be
labelled, or something more complicated.
2. A grid. Below, a 6 x 6 grid is used. The grid could be
multidimensional, or hexagonal, or even a grid of chaos tiles.
3. A code. Each code will produce a unique path. On a 50 x 50
grid, what path would result from a 12345678 code from a KT?

CONSTANT LENGTH TOURS
by Ed Pegg Jr.
Leonhard Euler was the first to find a closed tour of a chessboard by a
KT. Other pieces, more exotic, exist in the realm of Fairy
Chess. Until now, their tour
potential hasn’t been studied.
I’ll start with definitions, most of them standard Graph Theory
terms.
Point (vertex, node,
junction, cell)
Line (edge, arc, branch)
Two points are adjacent
(linked) if they are joined by a line.
A loop links a point to
itself. [None of the graphs in this paper contain loops.]
A line is incident to the points it joins.
The degree of a point is the number of lines incident to it.
Lattice - a graph where all
points are midpoints of tiles in a regular tiling. [I’ll deal with square tilings.]
A graph is connected if
there exists a sequence of points and lines from any point to any other point.
A Hamiltonian cycle is a
loopless, connected graph where every point of the graph has degree 2.
A Hamiltonian path is a connected graph of N points with N-2 points of degree 2
and 2 points of degree 1.
A Re-entrant knights tour is
a Hamiltonian cycle on an 8 x 8 lattice where each line has length.
Board: m x n lattice
of squares.
(Closed) Tour: A
Hamiltonian cycle on a lattice.
Open Tour: A
Hamiltonian path on a lattice.
Leaper: A KT is a
(1,2) leaper. In the same fashion, (2,3) leapers and (1,4) leapers exist.
Constant Length Tour:
A tour where every line has a constant length, c.
For c= sqrt(5),
we get KT moves. Question: What c’s allow a tour of the 8 x 8
board? Answer: The only c’s that work are c=1, c= sqrt(5), and
c=5. No tour exists on the 9 x 9 board, due to parity. For the 10 x 10 board, c=1, c= sqrt(5), c=
sqrt(13), c= sqrt(17), and c=5 are the only c’s that allow a constant length tour.
C = 1 corresponds to the
(0,1) leaper and is called a Prince.
C = sqrt(5) corresponds to
the (1,2) leaper and is called a KT.
C = sqrt(13) corresponds to
the (2,3) leaper and is called a Zebra [traditional Fairy Chess]. C = sqrt(17) corresponds to the (1,4) leaper
and is called a Giraffe.
Note that C = sqrt(a^2 + b^2) corresponds to a (a,b) leaper.
The standard puzzle seen in puzzle books involves the idea of
parity. An example of a parity argument:
Prove that a KT cannot make a closed tour of an n x n chessboard, where n is
odd. Proof: fill in the board
with a checkerboard colouring. The KT will start on one of the two
colours, let it be white. After an
even number of moves, the KT will be on a white cell. The closed tour has an odd number of
cells. Since a closed tour would
require the KT to land on its starting cell after an odd number of moves, the
tour is impossible.
We will now prove:
1. There is no closed tour for a
(1,2) leaper [KT] on a 4 x n board.
2. There is no open tour for a (1,2) leaper on a 4 x 4
board.
3. There is no open tour for a (1,4) leaper on an 8 x 8
board.
4. There is no open tour for a (2,3) leaper on an 8 x 8
board.
5. There is no open tour for a (2,3) leaper on a 9 x 9
board.
6. There is no open tour for a (2,3) leaper on an 11 x 11
board.
7. There is no open tour for a (2,3) leaper on a 12 x 12
board.
Note that the
nonexistence of an open tour implies the nonexistence of a closed tour.
1.
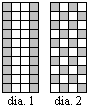 There is no closed tour for
the (1,2) leaper [KT] on a 4 x n board.
Proof by contradiction: Suppose such a tour existed. As can
be seen in diagram 1, every grey point (cell) is adjacent to two clear points.
A grey point is not adjacent to a grey point. Since half the tour consists of
grey points, the tour must look something like grey white grey white
.... white grey, where the first and last grey cells are the same
cell. Thus, every other move is a
clear point. As can be seen in
diagram 2, grey points are adjacent only to clear points.
Every other move must be a clear point. By combining these two
results, we get a contradiction; namely, that one fourth of the points support
one half of the total moves. The
idea of this proof is used several times in the course of this paper.
There is no closed tour for
the (1,2) leaper [KT] on a 4 x n board.
Proof by contradiction: Suppose such a tour existed. As can
be seen in diagram 1, every grey point (cell) is adjacent to two clear points.
A grey point is not adjacent to a grey point. Since half the tour consists of
grey points, the tour must look something like grey white grey white
.... white grey, where the first and last grey cells are the same
cell. Thus, every other move is a
clear point. As can be seen in
diagram 2, grey points are adjacent only to clear points.
Every other move must be a clear point. By combining these two
results, we get a contradiction; namely, that one fourth of the points support
one half of the total moves. The
idea of this proof is used several times in the course of this paper.
2.
 There is no open tour for a
(1,2) leaper on a 4 x 4 board.
There is no open tour for a
(1,2) leaper on a 4 x 4 board.
Proof A:
Examine the black points and grey points of diagram 3. The
corner grey points are adjacent only to the interior grey points,
the same applies to the black corner points. A closed tour is thus
impossible, since these two colours are closed to the rest of the
board. However, we have the leeway
of a spare move at the beginning and end of an open tour. We can start
with a black corner, eventually make a move from a black interior point
to the dot points and clear points, move to a grey interior point,
and finish the tour. Unfortunately, it is impossible to move directly
from a dot point to a clear point. So an open tour is impossible.
Proof B: This proof exploits the idea of Proof 1. Colour
the outer columns as shown in diagram 4.
A closed tour is impossible, as described in Proof 1. However, an open tour is possible on a 4 x n
board, provided the move sequence looks something like the following: grey
white grey...white grey grey-white ... grey white grey. If we colour the top and bottom rows, we
reach the same conclusion. Combining these, a tour is possible as long as
we move from a white point in diagram 5 to another white
point. This is impossible.
3.
 There is no open tour for a
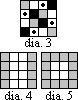
(1,4) leaper on an 8 x 8 board. Proof A:
Examine diagram 6. Borrowing a term from Cartesian coordinants, examine
the eight black points in the first and third quadrants. They are
adjacent only to black points in the second and fourth
quadrants. Similarly, the
grey points in the second and fourth quadrants are adjacently only to
grey points in the first and third quadrants. From here on, the
proof is identical to the proof in 2A.
There is no open tour for a
(1,4) leaper on an 8 x 8 board. Proof A:
Examine diagram 6. Borrowing a term from Cartesian coordinants, examine
the eight black points in the first and third quadrants. They are
adjacent only to black points in the second and fourth
quadrants. Similarly, the
grey points in the second and fourth quadrants are adjacently only to
grey points in the first and third quadrants. From here on, the
proof is identical to the proof in 2A.
Proof B:
Colour the board as shown in diagram 7.
The grey points are adjacent only to clear and dot
points. The closed tour is
impossible, see proof 1. An open
tour might be possible if we move from a non-grey point to a
non-grey point midway through the tour. Rotate the diagram 90
degrees, and make the same observations.
A tour is possible if two dot points are tour-adjacent. But they aren’t, so there isn’t an open
tour.
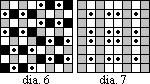
 4. There is no open tour for a (2,3) leaper on an 8 x 8 board.
4. There is no open tour for a (2,3) leaper on an 8 x 8 board.
Proof: In diagram 8, each grey point has degree 2, unless it marks the
beginning or end of a tour, in which case it can have degree 1. The
grey points are adjacent only to dot points. The
grey points require at least (14*2 + 2*1 = 30) lines, but the
dot points can only accept (12*2 = 24) of these lines. An open tour
is thus impossible.
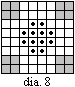
4.
 There is no open tour for a
(2,3) leaper on a 9 x 9 board.
There is no open tour for a
(2,3) leaper on a 9 x 9 board.
Proof: In diagram 9, each black point is adjacent to two
dot points. Each grey point is adjacent to at least one
dot point. The black and grey points require at least (
(16*2 + 16*1)/2 = 24) dot points, but there are only 21 dot points,
so the open tour is impossible.
A similar
colouring scheme is useful for showing the impossibility of (a,b) leapers on
small boards.
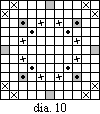 6. There is no open tour for a (2,3) leaper on an 11 x 11 board.
6. There is no open tour for a (2,3) leaper on an 11 x 11 board.
Proof: First, note that this is an odd board. Due to parity, the
grey points and X points can neither begin nor end the open
tour. Next, note that the
X points are adjacent only to dot points and squiggle
points. During the course of the
tour, we must have the sequence squiggle X dot X squiggle four
times. Now look at the
grey points. As far as the
tour is concerned, the grey points cannot be adjacent to dot points,
so they must be adjacent to the greydot points. Since each grey point has degree two, we
have a closed loop: grey greydot grey greydot grey greydot grey greydot. The tour is impossible.
This problem
was first solved by Dan Cass.
7.
 There is no open tour for a
(2,3) leaper on a 12 x 12 board. Proof:
First, note that a closed tour is impossible. Each
greysquiggle point has degree 2 and is only adjacent to dot
points. There are 36 greysquiggle points and 36 dot points,
and thus we have a closed system.
There is no open tour for a
(2,3) leaper on a 12 x 12 board. Proof:
First, note that a closed tour is impossible. Each
greysquiggle point has degree 2 and is only adjacent to dot
points. There are 36 greysquiggle points and 36 dot points,
and thus we have a closed system.
Now then, using the
methodology in Proof 1, note that the gray-shaded points are adjacent only to
the white-shaded points. Turn the
diagram 90 degrees and note the same thing. Combining, an open tour is possible only if
we can move from a dot point to a dot point midway through the
tour. We can! But this use of the only free move leads to
the same closed system described above.
Thus the open tour is impossible.
|
|
Warnsdorff’s rule
In the beginning of the 19th century a practical method for
solving the KTs tour emerged. In
“Des Rösselsprungs einfachste und allgemeinste Lösung” (Schmalkalden, 1823) H. C.
Warnsdorff presented his method of constructing KTs tours. The aim is to avoid creating dead ends - cells from which the KT
cannot get further without getting to an already visited cell. For that reason the possible cellss to be
chosen next are examined before every move.
One counts the number of free new choices - entrances - every one of
them has, and then moves to the square with the lowest number of new choices.
(Example see [1] ). Warnsdorff’s rule is heuristic. Theoretically there are objections [2],
but on a normal 8*8 cell board the rule works just fine. |
|
The Java
applet on this page demonstrates the efficiency of Warnsdorff’s rule: 1.
Click on any starting cell
of your choice (mouse left). The
numbers of free entrances to the cellss of the next legal move will be
displayed. Click on the one with the lowest
number, and continue this way until the whole board is covered and the KTs
tour completed. In many cases there
are equal choices and sometimes one might spare a cell with the lowest number
(in order to have it as the end cell of a re-entrant tour). There is a certain limited freedom of
choice, but cellss with one entrance are due to be visited
at once - otherwise they will turn into dead ends. One such cell can serve as ending cell for
the whole tour, two means trouble. 2.
Back: Click with mouse
right on an already visited cel, and the tour will be shortened so that the
move from that cell can be redone. Try it and discover how
easy it is to solve the KTs tour with the help of Warnsdorff’s rule! |
|
1. Example: Take a look at a
cell in a corner of the board. From
such a cell a KT can jump to only two other cells. And the cell in the corner can be reached
only from these two other cells - the cell in the corner has two
“entrances”. When a KT during a tour
happens to visit any of these entrances, it is almost bound to visit the corner
cell next. If the KT doesn’t do that,
it has used up one of the two free entrances of the corner cell - and thus
turned that cell into a dead end; the corner cell can still be reached later,
but there will no longer be any unused way out.
During a KTs tour the number of free entrances to all cells of the board
are gradually used up. Warnsdorff’s
rule serves to direct the KT to the cells with the least numbers of free
entrances left - before these cells have turned into dead ends.
2. Warnsdorff’s rule gives
solutions, but not all possible solutions (One can make moves opposing the rule
and yet get a complete tour). The rule
possesses a trait of arbitrariness; there is often a choice between equal
alternatives. And on really big boards
the rule runs into trouble. Warnsdorff
scarcely had the possibilities to explore this, but Arnd Roth
at the Max-Planck-institut für Medizinische Forschung presents an investigation
of this in "The
Problem of the Knight"
A strategy game
for you and your computer
Take the Challenge
A chessboard is set with two KTs: one black, one white. Yours is the white KT and you take the first
move. You alternate turns with the
computer, but you lose if it’s your turn and you can’t move. Sounds easy, right?
The pieces move just like knights in ordinary chess, but the trick is
that cells disappear from the board when pieces pass through them. Once you’ve been to a cell, neither you nor
the computer can go there again.
One strategy is to try and stay free so that you’ll never be caught
without a possible move. Another is to
try and head off the computer KT so that it will be left without anywhere to
go. The computer does a little of each
and plays a decent game.
Once the game is loaded, you simply point and click on the board to
move. After the game ends, click the
red button to play again.
KTs’ Tourney requires version 5 of
Macromedia’s Flash Player. If you don’t
have the plug-in, you can download
it for free.
About this Game
The KTs Tour is a
classic logic puzzle in the form of a chess problem: Is it possible for a chess
KT to move through every cell on the board without revisiting any? The answer
for the usual 8 x 8 chessboard is yes, but the general question for arbitrary
board sizes has interested mathematicians working in the area of graph
theory. See, for instance, Mark Keen's paper on the
subject. There are several on-line implementations of the original
problem.
KT’ Tourney is a two-player
generalization of the KTs Tour
which has been suggested by enough people that it’s hard to name one
inventor. This implementation of it is
©2001 by P.D. Magnus.
|
WebChess (Gnuchess) |
|
|
|
CoffeeHouse - Java interface to Internet Chess Club
Grandmaster Java Chess
Viewer
If
you can’t see the frames at the left please click here
This page was
designed and is maintained by David Roberts, d@dial.pipex.com
©1997, 1998 David Roberts.

Links to More Knight Tours
Hi, You asked if I could give you a link. I would
like to share http://www.borderschess.org/KnightTour.htm (The
Knight's Tour). KnightTour.htm is in English and in German in order
to reach a larger audience. It describes how to solve open and closed knight
tours along with other interesting knight tour puzzles such as closed knight's
tour cube, magic/semi-magic squares, tessellations, and knight's tour art. You will find many
new items and updates on my web page that will enhance your Chesmayne Chess
Dictionary. Please feel free to make the necessary changes and updates to
your section of Knight - Tour in your dictionary. You may want to
change the reference of Knight - Tour on http://chesmayn.valuehost.co.uk/K.htm to
"Knight - Tours". Also, on http://chesmayn.valuehost.co.uk/Knights-Tour.htm,
please change the title of "Knights Tour" to "Knight
Tours". I have a new title banner and home-made navigation
buttons for each page on KnightTour.htm. Feel free to copy them for your
use. I've made several corrections to many of my web pages. Please
update your site with the new changes.
Nice Site you have at http://chesmayn.valuehost.co.uk.
I think it will become very successful on the Internet. Cordially, Dan.
If
you get a chance, take a fresh look at my Knight Tours web site: www.borderschess.org/KnightTour.htm
to see many new items. I am applying for a patent on Springer
Geometry. Springer is the German word for "Knight" in
English. Springer Geometry is the geometry of polygons created by closed
knight tours. I hope you enjoy my new additions. A patent search
has already been completed, so now the patent attorney is ready to send my
ideas in for a Utility Patent. I am currently preparing information to
send to Springer-Verlag, a math & science book publishing company, to see
if they would be interested in publishing a book about my Knight Tours and
Springer Geometry. Their logo is the chess knight.
I've
also finally decided to let my computer solve additional knight
tours using Mathematica and code written by Dr. Colin Rose and modified by
Michael Taktikos from Germany, and from myself. The code has
solved all unique 6x6 closed knight tours (9862 total). I have
included printouts on my web site of various other closed and symmetrical tours
for smaller size boards. Anyway, check it out and see if you like the new
stuff. Let me know if you have any ideas, comments, or criticisms.
Keep
in touch. Cheers,
Dan
Links
to More Knight Tours
www.BordersChess.org/KnightTour.htm
homepages.stayfree.co.uk/gpj/ktn.htm
www.velucchi.it/mathchess/knight.htm
enchantedmind.com/puzzles/knights/knight.htm
www.helsinki.fi/~vahaaho/KnightsTour/tour.html
www.helsinki.fi/~vahaaho/KnightsTour/doc/doc.html
student.lssu.edu/~gbharadw/java/knight.html
www.tcp-ip.or.jp/~toshio-t/K_tour.html
www.npac.syr.edu/projects/tutorials/Java/examples/KnightTour/Knight.html
w1.859.telia.com/~u85905224/knight/knight.htm
w1.859.telia.com/~u85905224/knight/eknight.htm
home.earthlink.net/~tfiller/knight.htm#
www.mactech.com/articles/mactech/Vol.14/14.11/TheKnight'sTour/
www.worle.com/chess/solution.htm
www.worle.com/chess/knight.htm#top
www.tri.org.au/knightframe.html
members.attcanada.ca/~ptah/knights.htm
www.inficad.com/~ecollins/knights-tour.htm
www.delphiforfun.org/Programs/knight's_tour.htm
www.uweb.ucsb.edu/~rjr/KnightsTour.html
mail.stuy.edu/pipermail/csteam/2000-October/000001.html
hercule.csci.unt.edu/~ian/papers/knight2.html
hercule.csci.unt.edu/~ian/papers/knight3.html
www.theory.csc.uvic.ca/~cos/inf/misc/Knight.html
ourworld.compuserve.com/homepages/John_Katrin_Sharp/Articles.htm
www.mathpuzzle.com/leapers.htm
www.reflexive.net/james/OldSoftware/
www.hctc.com/~dtriplet/link.htm#Puzzles
mathworld.wolfram.com/KnightsTour.html
mathworld.wolfram.com/KnightsTourGraph.html
www.math.niu.edu/~rusin/known-math/99/knights
www.singaren.net.sg/DAC/projects/magic.html
www.combinatorics.org/Volume_3/Abstracts/v3i1r5.html
www.combinatorics.org/Volume_3/Comments/v3i1r5.html
cs.anu.edu.au/~bdm/papers/knights.ps.gz
www.ex.ac.uk/~dregis/DR/tour2.html









![[Knights' Tourney]](Knights-Tour_files/image049.gif)